题目内容
已知α、β、γ是三个不同的平面,命题“α∥β,且α⊥γ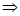 β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
2
解析

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
题目内容
已知α、β、γ是三个不同的平面,命题“α∥β,且α⊥γ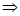 β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
β⊥γ”是真命题,如果把α、β、γ中的任意两个换成直线,另一个保持不变,在所得的所有新命题中,真命题的个数是________.
2
解析

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案