题目内容
(2012•泰州二模)已知α,β是方程x2-x-1=0的两个根,且α<β.数列{an},{bn}满足a1=1,a2=β,an+2=an+1+an(n∈N*),bn=an+1-αan.
(1)求b2-a2的值;
(2)证明:数列{bn}是等比数列;
(3)设c1=1,c2=-1,cn+2+cn+1=cn(n∈N*),证明:当n≥3时,an=(-1)n-1(αcn-2+βcn).
(1)求b2-a2的值;
(2)证明:数列{bn}是等比数列;
(3)设c1=1,c2=-1,cn+2+cn+1=cn(n∈N*),证明:当n≥3时,an=(-1)n-1(αcn-2+βcn).
分析:(1)α,β是方程x2-x-1=0的两个根,利用韦达定理与b2=a3-αa2,即可求得b2-a2的值;
(2)反复利用an+2=an+1+an,可求得
=β(定值),b1=a2-αa1=β-α≠0,从而可证数列{bn}是等比数列;
(3)由(2)知an+1-αan=(β-α)βn-1,①又an+1=an+an-1,α+β=1,αβ=-1,可求得得an+1-βan=0②,从而可得an=βn-1,最后可证得n≥3时,
=β,从而可使结论得证.
(2)反复利用an+2=an+1+an,可求得
| bn+1 |
| bn |
(3)由(2)知an+1-αan=(β-α)βn-1,①又an+1=an+an-1,α+β=1,αβ=-1,可求得得an+1-βan=0②,从而可得an=βn-1,最后可证得n≥3时,
| (-1)n(αcn-1+βcn+1) |
| (-1)n-1(αcn-2+βcn) |
解答:解:(1)∵α,β是方程x2-x-1=0的两个根,
∴α+β=1,αβ=-1,β2=β+1,由题意知,b2=a3-αa2,
∴b2-a2=2.
(2)证明:∵
=
=
=
=
=
=β,
又b1=a2-αa1=β-α≠0,
∴数列{bn}是首项为β-α,公比为β等比数列;
(3)由(2)知an+1-αan=(β-α)βn-1,①
又an+1=an+an-1,α+β=1,αβ=-1,
∴an+1=(α+β)an-αβan-1,
an+1-βan=α(an-βan-1),由a2-βa1=0,α≠0,得an+1-βan=0②
由①②得:an=βn-1,
下面我们只要证明:n≥3时,(-1)n-1(αcn-2+βcn)=βn-1.
∵cn+2+cn+1=cn,β2=β+1,
∴
=-
=-
=-
=-
=-
=β
∴n≥3时,(-1)n-1(αcn-2+βcn)=βn-1,即n≥3时,an=(-1)n-1(αcn-2+βcn)(证毕).
∴α+β=1,αβ=-1,β2=β+1,由题意知,b2=a3-αa2,
∴b2-a2=2.
(2)证明:∵
| bn+1 |
| bn |
| an+2-αan+1 |
| an+1-αan |
| an+1+an-αan+1 |
| an+1-αan |
| (1-α)an+1+an |
| an+1-αan |
| βan+1+an |
| an+1-αan |
| βan+1-αβan |
| an+1-αan |
又b1=a2-αa1=β-α≠0,
∴数列{bn}是首项为β-α,公比为β等比数列;
(3)由(2)知an+1-αan=(β-α)βn-1,①
又an+1=an+an-1,α+β=1,αβ=-1,
∴an+1=(α+β)an-αβan-1,
an+1-βan=α(an-βan-1),由a2-βa1=0,α≠0,得an+1-βan=0②
由①②得:an=βn-1,
下面我们只要证明:n≥3时,(-1)n-1(αcn-2+βcn)=βn-1.
∵cn+2+cn+1=cn,β2=β+1,
∴
| (-1)n(αcn-1+βcn+1) |
| (-1)n-1(αcn-2+βcn) |
| αcn-1+βcn-1-βcn |
| αcn-2+βcn |
| cn-1-βcn |
| αcn-2+βcn |
| cn-2-cn-βcn |
| αcn-2+βcn |
| cn-2-(1+β)cn |
| αcn-2+βcn |
| -αβcn-2-β2cn |
| αcn-2+βcn |
∴n≥3时,(-1)n-1(αcn-2+βcn)=βn-1,即n≥3时,an=(-1)n-1(αcn-2+βcn)(证毕).
点评:本题考查数列递推式,突出考查等比关系的确定,考查抽象思维与逻辑推理的能力,考查转化思想、化归思想与综合运算能力,属于难题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
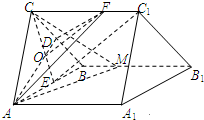 (2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.
(2012•泰州二模)如图,三棱柱ABC-A1B1C1中,D、E分别是棱BC、AB的中点,点F在棱CC1上,已知AB=AC,AA1=3,BC=CF=2.