题目内容
已知数列{an}中a1=1,且a2k=a2k-1+(-1)k,a2k+1=a2k+3k,其中k=1,2,3,….(I)求a3,a5;
(II)求{an}的通项公式.
【答案】分析:(I)由题意知a2=a1+(-1)1=0,a3=a2+31=3.a4=a3+(-1)2=4,a5=a4+32=13.
(II)由题设条件知a2k+1-a2k-1=3k+(-1)k,a2k-1-a2k-3=3k-1+(-1)k-1,由此得a2k+1-a1= (3k-1)+
(3k-1)+ [(-1)k-1],于是a2k+1=
[(-1)k-1],于是a2k+1=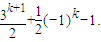 由此可求出{an}的通项公式.
由此可求出{an}的通项公式.
解答:解:(I)a2=a1+(-1)1=0,
a3=a2+31=3.
a4=a3+(-1)2=4,
a5=a4+32=13,
所以,a3=3,a5=13.
(II)a2k+1=a2k+3k
=a2k-1+(-1)k+3k,
所以a2k+1-a2k-1=3k+(-1)k,
同理a2k-1-a2k-3=3k-1+(-1)k-1,
a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)++(a3-a1)
=(3k+3k-1++3)+[(-1)k+(-1)k-1++(-1)],
由此得a2k+1-a1= (3k-1)+
(3k-1)+ [(-1)k-1],
[(-1)k-1],
于是a2k+1=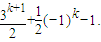
a2k=a2k-1+(-1)k=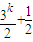 (-1)k-1-1+(-1)k=
(-1)k-1-1+(-1)k=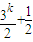 (-1)k=1.
(-1)k=1.
{an}的通项公式为:
当n为奇数时,an=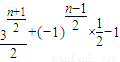 ;
;
当n为偶数时,
点评:本题主要考查数列,等比数列的概念和基本知识,考查运算能力以及分析、归纳和推理能力.
(II)由题设条件知a2k+1-a2k-1=3k+(-1)k,a2k-1-a2k-3=3k-1+(-1)k-1,由此得a2k+1-a1=
 (3k-1)+
(3k-1)+ [(-1)k-1],于是a2k+1=
[(-1)k-1],于是a2k+1=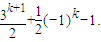 由此可求出{an}的通项公式.
由此可求出{an}的通项公式.解答:解:(I)a2=a1+(-1)1=0,
a3=a2+31=3.
a4=a3+(-1)2=4,
a5=a4+32=13,
所以,a3=3,a5=13.
(II)a2k+1=a2k+3k
=a2k-1+(-1)k+3k,
所以a2k+1-a2k-1=3k+(-1)k,
同理a2k-1-a2k-3=3k-1+(-1)k-1,
a3-a1=3+(-1).
所以(a2k+1-a2k-1)+(a2k-1-a2k-3)++(a3-a1)
=(3k+3k-1++3)+[(-1)k+(-1)k-1++(-1)],
由此得a2k+1-a1=
 (3k-1)+
(3k-1)+ [(-1)k-1],
[(-1)k-1],于是a2k+1=
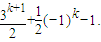
a2k=a2k-1+(-1)k=
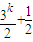 (-1)k-1-1+(-1)k=
(-1)k-1-1+(-1)k=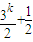 (-1)k=1.
(-1)k=1.{an}的通项公式为:
当n为奇数时,an=
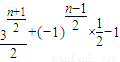 ;
;当n为偶数时,

点评:本题主要考查数列,等比数列的概念和基本知识,考查运算能力以及分析、归纳和推理能力.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目