题目内容
在Rt△ABC中,AB=6,AC=8,∠A=90°,若△ABC所在平面α外的一点P到三个顶点A、B、C的距离都为13,点P在α内的射影是O,则线段PO的长为( )
分析:由Rt△ABC中,AB=6,AC=8,∠A=90°,知BC=10,由△ABC所在平面α外的一点P到三个顶点A、B、C的距离都为13,点P在α内的射影是O,知Rt△ABC的外心是O,故O是BC的中点,AO=BO=CO=5,由此能求出PO.
解答: 解:∵Rt△ABC中,AB=6,AC=8,∠A=90°,
解:∵Rt△ABC中,AB=6,AC=8,∠A=90°,
∴BC=
=10,
∵△ABC所在平面α外的一点P到三个顶点A、B、C的距离都为13,
点P在α内的射影是O,
∴AO=BO=CO,
∴Rt△ABC的外心是O,故O是BC的中点,
∴AO=BO=CO=5,
∴PO=
=12.
故选A.
 解:∵Rt△ABC中,AB=6,AC=8,∠A=90°,
解:∵Rt△ABC中,AB=6,AC=8,∠A=90°,∴BC=
| 62+82 |
∵△ABC所在平面α外的一点P到三个顶点A、B、C的距离都为13,
点P在α内的射影是O,
∴AO=BO=CO,
∴Rt△ABC的外心是O,故O是BC的中点,
∴AO=BO=CO=5,
∴PO=
| 132-52 |
故选A.
点评:本题考查点、线、面间距离的计算,是基础题.解题的关键步骤是准确判断出Rt△ABC的外心是O,即O是BC的中点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在Rt△ABC中,∠A=90°,|
|=1,则
•
的值为:( )
| AB |
| AB |
| BC |
| A、1 | B、-1 |
| C、1或-1 | D、不能确定 |
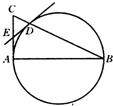 15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.
15、如图,在Rt△ABC中,∠A=90°,以AB为直径的半圆交BC于D,过D作圆的切线交AC于E.