题目内容
已知命题p:m<0,命题q:?x∈R,x2+mx+1>0成立,若“p∧q”为真命题,则实数m的取值范围是
| A.[-2,0] |
| B.(0,2) |
| C.(-2,0) |
| D.(-2,2) |
C
解析由?x∈R,x2+mx+1>0成立,Δ=m2-4<0,
所以-2<m<2.因为“p∧q”为真命题,则p,q都为真命题,
故 ,即-2<m<0.
,即-2<m<0.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
若命题“ 使得
使得 ”为假命题,则实数
”为假命题,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
设 是平面
是平面 内两条不同的直线,
内两条不同的直线, 是平面
是平面 外的一条直线,则
外的一条直线,则 且
且 是
是 的( )
的( )
| A.充要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
“ ”是“函数
”是“函数 的最小正周期为
的最小正周期为 ”的( ).
”的( ).
| A.充分必要条件 | B.充分不必要条件 |
| C.必要不充分条件 | D.既不充分又必要条件 |
命题“对任意 ,都有
,都有 ”的否定是( )
”的否定是( )
A.存在 ,使得 ,使得 | B.不存在 ,使得 ,使得 |
C.存在 ,使得 ,使得 | D.对任意 ,都有 ,都有 |
下列命题正确的是
A.“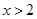 ”是“ ”是“ ”的必要不充分条件 ”的必要不充分条件 |
B.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 则 则 ” ” |
C.若 为假命题,则 为假命题,则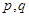 均为假命题 均为假命题 |
D.对于命题 : : ,使得 ,使得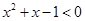 ,则 ,则 : : 均有 均有 |
给出下列三个结论:(1)若命题 为真命题,命题
为真命题,命题 为真命题,则命题“
为真命题,则命题“ ”为真命题;(2)命题“若
”为真命题;(2)命题“若 ,则
,则 或
或 ”的否命题为“若
”的否命题为“若 ,则
,则 或
或 ”;(3)命题“
”;(3)命题“ ”的否定是“
”的否定是“ ”.则以上结论正确的个数为( )
”.则以上结论正确的个数为( )
| A.3个 |
| B.2个 |
| C.1个 |
| D.0个 |
设集合A={x∈R|x-2>0},B={x∈R|x<0},C={x∈R|x(x-2)>0},则“x∈A∪B”是“x∈C”的( )
| A.充分而不必要条件 |
| B.必要而不充分条件 |
| C.充分必要条件 |
| D.既不充分也不必要条件 |
已知 是定义在R上的偶函数,且以2为周期,则“
是定义在R上的偶函数,且以2为周期,则“ 为
为 上的增函数”是“
上的增函数”是“ 为
为 上的减函数”的( )
上的减函数”的( )
| A.既不充分也不必要的条件 |
| B.充分而不必要的条件 |
| C.必要而不充分的条件 |
| D.充要条件 |