题目内容
(2012•珠海一模)在平面直角坐标系中,已知两圆C1:(x-1)2+y2=25和C2:(x+1)2+y2=1,动圆在C1内部且和圆C1相内切并和圆C2相外切,动圆圆心的轨迹为E.
(1)求E的标准方程;
(2)点P为E上一动点,点O为坐标原点,曲线E的右焦点为F,求|PO|2+|PF|2的最小值.
(1)求E的标准方程;
(2)点P为E上一动点,点O为坐标原点,曲线E的右焦点为F,求|PO|2+|PF|2的最小值.
分析:(1)根据两圆外切和内切的判定,圆心距与两圆半径和差的关系,设出动圆半径为r,消去r,根据圆锥曲线的定义,即可求得动圆圆心D的轨迹,进而可求其方程.
(2)解法一:首先有点P在E上,根据椭圆的参数方程表示出P的坐标,再表达出|PE|,|PO|,利用三角函数的性质,从而求出最大值;
解法二:设P(x,y),x∈[-3,3],先利用x,y表示出|PO|2+|PF|2=2x2-2x+2y2+1,再利用点P(x,y)满足
+
=1,将原式化成|PO|2+|PF|2=
(x-
)2+
,最后利用二次函数的性质即可求出|PO|2+|PF|2的最小值.
(2)解法一:首先有点P在E上,根据椭圆的参数方程表示出P的坐标,再表达出|PE|,|PO|,利用三角函数的性质,从而求出最大值;
解法二:设P(x,y),x∈[-3,3],先利用x,y表示出|PO|2+|PF|2=2x2-2x+2y2+1,再利用点P(x,y)满足
| x2 |
| 9 |
| y2 |
| 8 |
| 2 |
| 9 |
| 9 |
| 2 |
| 25 |
| 2 |
解答:解:(1)设动圆圆心D(x,y),半径为r,由题意,动圆内切于圆C1,且和圆C2相外切,
∵|DC1|=5-r,|DC2|=1+r,
∴|DC1|+|DC2|=6>|C1C2|=2
∴D点的轨迹图形E是C1、C2为焦点的椭圆 (3分)
其中2a=6,c=1,
∴a=3,b2=a2-c2=8(4分)
∴D点的轨迹图形E:
+
=1(6分)
(2)解法一:由题设知F(1,0),
∵P在E上
∴设P(3cosθ,2
sinθ),θ∈[0,2π](8分)
则|PF|2=(3cosθ-1)2+(2
sinθ)2=9cos2θ-6cosθ+1+8sin2θ=cos2θ-6cosθ+9(9分)
|PO|2=(3cosθ)2+(2
sinθ)2=cos2θ+8(10分)
∴|PF|2+|PO|2=2cos2θ-6cosθ+17=2(cosθ-
)2+
(12分)
∵cosθ∈[-1,1],
∴当cosθ=1时,|PO|2+|PF|2的最小值为13.(14分)
解法二:设P(x,y),x∈[-3,3],(7分)
则|PO|2=x2+y2,(8分)|PF|2=(x-1)2+y2(9分)
∴|PO|2+|PF|2=2x2-2x+2y2+1(10分)
点P(x,y)满足
+
=1,
∴y2=8(1-
),(11分)
∴|PO|2+|PF|2=
(x-
)2+
(12分)
∵x∈[-
,
],
∴当x=3时,|PO|2+|PF|2的最小值为13.(14分)
∵|DC1|=5-r,|DC2|=1+r,
∴|DC1|+|DC2|=6>|C1C2|=2
∴D点的轨迹图形E是C1、C2为焦点的椭圆 (3分)
其中2a=6,c=1,
∴a=3,b2=a2-c2=8(4分)
∴D点的轨迹图形E:
| x2 |
| 9 |
| y2 |
| 8 |
(2)解法一:由题设知F(1,0),
∵P在E上
∴设P(3cosθ,2
| 2 |
则|PF|2=(3cosθ-1)2+(2
| 2 |
|PO|2=(3cosθ)2+(2
| 2 |
∴|PF|2+|PO|2=2cos2θ-6cosθ+17=2(cosθ-
| 3 |
| 2 |
| 25 |
| 2 |
∵cosθ∈[-1,1],
∴当cosθ=1时,|PO|2+|PF|2的最小值为13.(14分)
解法二:设P(x,y),x∈[-3,3],(7分)
则|PO|2=x2+y2,(8分)|PF|2=(x-1)2+y2(9分)
∴|PO|2+|PF|2=2x2-2x+2y2+1(10分)
点P(x,y)满足
| x2 |
| 9 |
| y2 |
| 8 |
∴y2=8(1-
| x2 |
| 9 |
∴|PO|2+|PF|2=
| 2 |
| 9 |
| 9 |
| 2 |
| 25 |
| 2 |
∵x∈[-
| 2 |
| 2 |
∴当x=3时,|PO|2+|PF|2的最小值为13.(14分)
点评:本题主要考查两圆的位置关系及判定方法和椭圆的定义、标准方程,椭圆的参数方程,考查最值问题.

练习册系列答案
相关题目
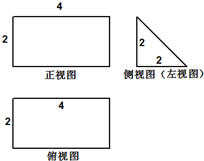 (2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( )
(2012•珠海一模)如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为( ) (2012•珠海一模)如图,在△ABC中,已知
(2012•珠海一模)如图,在△ABC中,已知