题目内容
下列说法中
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.
③离心率为
,长轴长为8的椭圆标准方程为
+
=1;
④若3<k<4,则二次曲线
+
=1的焦点坐标是(±1,0).
其中正确的为
①设定点F1(0,-3),F2(0,3),动点P(x,y)满足条件|PF1|+|PF2|=a(a>0),则动点P的轨迹是椭圆或线段;
②命题“每个指数函数都是单调函数”是全称命题,而且是真命题.
③离心率为
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
④若3<k<4,则二次曲线
| x2 |
| 4-k |
| y2 |
| 3-k |
其中正确的为
②④
②④
(写出所有真命题的序号)分析:①当a<6时,轨迹不存在.②根据全称命题的定义判断.③椭圆的焦点位置不确定,所以方程不确定.④当3<k<4,4-k>0>3-k曲线为双曲线,然后利用双曲线的方程确定c.
解答:解:①根据椭圆的定义可知,a>6,所以当a<6时,轨迹不存在,所以①错误.
②命题含有全称量词“每个”,所以命题是全称命题,且为真命题,正确.
③由题意知2a=8,所以a=4,由e=
=
,得c=2,所以b2=a2-c2=12,所以椭圆标准方程为
+
=1或
+
=1,所以③错误.
④当3<k<4,4-k>0>3-k曲线为双曲线,双曲线方程为
-
,焦点在x轴上,所以a2=4-k,b2=k-3,所以c2=a2+b2=1,即c=1,所以焦点坐标是(±1,0),所以④正确.
故答案为:②④
②命题含有全称量词“每个”,所以命题是全称命题,且为真命题,正确.
③由题意知2a=8,所以a=4,由e=
| c |
| a |
| 1 |
| 2 |
| x2 |
| 16 |
| y2 |
| 12 |
| y2 |
| 16 |
| x2 |
| 12 |
④当3<k<4,4-k>0>3-k曲线为双曲线,双曲线方程为
| x2 |
| 4-k |
| y2 |
| k-3 |
故答案为:②④
点评:本题主要考查各种命题的真假判断,综合性较强,涉及的知识点较多.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
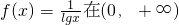 是减函数;
是减函数;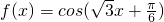 ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数;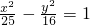 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5; 是减函数;
是减函数; ,则f(x)+f'(x)是奇函数;
,则f(x)+f'(x)是奇函数; 的一个焦点到渐近线的距离是5;
的一个焦点到渐近线的距离是5;