Question

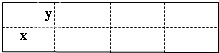
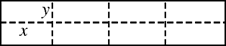
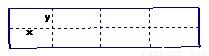
图是某水产养殖场的养殖大网箱的平面图，四周的实线为网衣为避免混养，用筛网（图中虚线）把大网箱隔成大小一样的小网箱．每个小网箱的长为x米，宽为y米．若大网箱的面积为160平方米，网衣的造价为112元/米，筛网的造价为96元/米，且大网箱的长与宽都不超过15米．
（Ⅰ）设总造价为W元，试求出W关于x的函数关系式；
（Ⅱ）小网箱的长、宽分别为多少米时，可使总造价最低？

Answer 1

分析：（1）利用已知条件列出面积然后写出利润表达式．
（2）通过函数的导数判断函数的单调性求出闭区间上的最小值即可．

解答：解：（1）依题意得：4x•2y=160，∴xy=20．…（1分）
∵4x≤15，且2y≤15，∴x≤

15

4

，y≤

15

2

．
又∵y=

20

x

≤

15

2

．所以

8

3

≤x≤

15

4

．…（3分）
∴W=（8x+4y）•112+（4x+6y）•96
=（8x+4×

20

x

）•112+（4x+6×

20

x

）•96
=1280（x+

16

x

） （

8

3

≤x≤

15

4

）…（7分）
（2）由（1）可知W′=1280（1-

16

x2

）=1280（

x2-16

x2

）
又∵x∈[

8

3

，

15

4

]，∴W′＜0 …（8分）
所以W（x）在[

8

3

，

15

4

]上单调递减． …（10分）
所以当x=

15

4

时，W最小，此时x=

15

4

，y=

16

3

．…（12分）
即当小网箱的长与宽分别为

15

4

米与

16

3

米时，可使总造价最低．…（13分）
（注：若用基本不等式时注意等号取不到，其解法请参照给分．）

点评：本题考查函数的解析式的求法，利用导数求解函数的最小值，考查分析问题解决问题的能力．