��Ŀ����
(��С������12��)��ͼ��ʾ��ijˮ����ֳ������ֳ�������ƽ��ͼ�����ܵ�ʵ��Ϊ���£�Ϊ�����������ɸ��(ͼ������)�Ѵ�������ɴ�Сһ����С���䣮
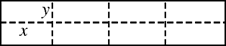
(1)������������Ϊ108ƽ���ף�ÿ��С����ij�x����y���Ϊ������ʱ������ʹΧ�ɵ�������ɸ���ܳ�����С��
(2)������������Ϊ160ƽ���ף����µ����Ϊ112Ԫ/�ף�ɸ�������Ϊ96Ԫ/�ף��Ҵ�����ij������������15�ף���С����ij�����Ϊ������ʱ����ʹ�������ͣ�
(1)ÿ��С����ij�����ֱ�Ϊ��4.5����3��ʱ��������ɸ�����ܳ�����С��
(2)��С����ij�����ֱ�Ϊ ����
����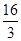 ��ʱ����ʹ�������ͣ�
��ʱ����ʹ�������ͣ�
��������
�����������1����ʵ������ת������ѧ���⣬���ֳ˻��Ƕ�ֵ���ҵȺ���ȡ�������û�������ʽ����ֵ��
��2����ʵ������ת������ѧ���⣬���ֳ˻��Ƕ�ֵ�����Ⱥ�ȡ�����������û�������ʽ����ֵ�����õ�����������������ֵ��
(1)��С����ij������ֱ�Ϊx��y�ף�ɸ���ܳ���ΪL��
������4x��2y��108����xy�� ��L��4x��6y. ����1��
��L��4x��6y. ����1��
��Ϊ4x��6y��2(2x��3y)��4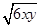 ��36������L��36. ������3��
��36������L��36. ������3��
���ҽ���2x��3yʱ���Ⱥų�����
�ⷽ����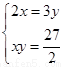 ��
��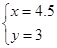 ����5��
����5��
��ÿ��С����ij�����ֱ�Ϊ��4.5����3��ʱ��������ɸ�����ܳ�����С��������6��
(2)�������ΪWԪ������4x��2y��160����xy��20. ����7��
��Ϊ4x��15,2y��15������x�� ��y��
��y��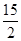 .
.
����Ϊy��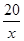 ��
��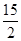 .
.
����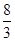 ��x��
��x�� .����8��
.����8��
W��(8x��4y)��112��(4x��6y)��96��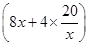 ��112��
��112��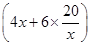 ��96��1 280
��96��1 280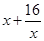 .����9��
.����9��
���ɵ�W(x)��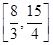 �ϵ����ݼ�������10��
�ϵ����ݼ�������10��
���Ե�x�� ʱ��W��С����ʱx��
ʱ��W��С����ʱx�� ��y��
��y��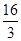 .����11��
.����11��
����С����ij�����ֱ�Ϊ ����
����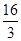 ��ʱ����ʹ�������ͣ�������12��
��ʱ����ʹ�������ͣ�������12��
���㣺��������Ҫ��������ʵ�������У����þ�ֵ����ʽ�����ֵ�����á�
���������������Ĺؼ������û�������ʽ����������ֵ��һ��ע��ʹ�õ�������һ��������������ȣ���ȻҲ�������ú�����˼�������õ���ֵ������Ҫ����ʹ�á�

 ��У����ϵ�д�
��У����ϵ�д�