题目内容
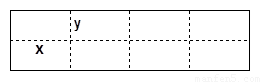
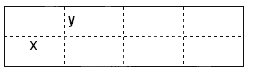
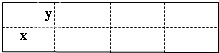
如图所示是某水产养殖场的养殖大网箱的平面图,四周的实线为网衣,为避免混养,用筛网(图中虚线)把大网箱隔成大小一样的小网箱.(1)若大网箱的面积为108平方米,每个小网箱的长x,宽y设计为多少米时,才能使围成的网箱中筛网总长度最小;
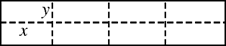
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的长、宽为多少米量,可使总造价最低?
分析:(1)将实际问题转化成数学问题,出现乘积是定值,且等号能取到,利用基本不等式求最值.
(2)将实际问题转化成数学问题,出现乘积是定值,但等号取不到,不能用基本不等式求最值,利用导数求函数单调性求最值.
(2)将实际问题转化成数学问题,出现乘积是定值,但等号取不到,不能用基本不等式求最值,利用导数求函数单调性求最值.
解答: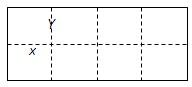 解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,
解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,
依题意4x•2y=108,即xy=
,S=4x+6y,
因为4x+6y=2(2x+3y)≥4
=36,所以S≥36,
当且仅当2x=3y时,等号成立,
解方程组
得
即每个小网箱的长与宽分别为与4.5米与3米时,网箱中筛网的总长度最小.
(2)设总造价为W元,则由4x•2y=160,得xy=20,
因为4x≤15,2y≤15,所以x≤
,y≤
,y=
≤
,∴
≤x≤
W=(8x+4y)•112+(4x+6y)•96=(8x+4×
)•112+(4x+6×
)•96=1280(x+
),
求导,可得W(x)在[
,
]上单调递减,所以当x=
时,W最小,此时x=
,y=
,
即当小网箱的长与宽分别为
米与
米时,可使总造价最低.
 解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,
解:(1)设小网箱的长、宽分别为x米、y米,筛网总长度为S,依题意4x•2y=108,即xy=
| 27 |
| 2 |
因为4x+6y=2(2x+3y)≥4
| 6xy |
当且仅当2x=3y时,等号成立,
解方程组
|
|
即每个小网箱的长与宽分别为与4.5米与3米时,网箱中筛网的总长度最小.
(2)设总造价为W元,则由4x•2y=160,得xy=20,
因为4x≤15,2y≤15,所以x≤
| 15 |
| 4 |
| 15 |
| 2 |
| 20 |
| x |
| 15 |
| 2 |
| 8 |
| 3 |
| 15 |
| 4 |
| 20 |
| x |
| 20 |
| x |
| 16 |
| x |
求导,可得W(x)在[
| 8 |
| 3 |
| 15 |
| 4 |
| 15 |
| 4 |
| 15 |
| 4 |
| 16 |
| 3 |
即当小网箱的长与宽分别为
| 15 |
| 4 |
| 16 |
| 3 |
点评:本题考查利用基本不等式请求函数的最值是一定注意使用的条件:一正;二定;三相等.

练习册系列答案
相关题目
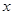 、纵边
、纵边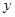 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?