题目内容
1.已知函数f(x)=$\left\{\begin{array}{l}\frac{2x+1}{{x}^{2}},x∈(-∞,-\frac{1}{2})\\ ln(x+1),x∈[-\frac{1}{2},+∞)\end{array}\right.$,g(x)=x2-4x-4,对于任意的a∈R,存在实数b使得f(a)+g(b)=0,则b的取值范围是( )| A. | [ln$\frac{1}{2}$,+∞) | B. | (-1,ln$\frac{1}{2}$] | C. | (-1,5) | D. | [-1,5] |
分析 利用基本不等式和对数函数的单调性,求出函数f(x)值域,进而根据存在a∈R使得f(a)+g(b)=0,得到g(b)=b2-4b-4≤1,解不等式可得实数b的取值范围.
解答 解:当x<-$\frac{1}{2}$时,2x+1<0,令t=2x+1,则t<0,且x=$\frac{t-1}{2}$,
则$\frac{2x+1}{{x}^{2}}$=$\frac{t}{(\frac{t-1}{2})^{2}}$=$\frac{t}{\frac{1}{4}({t}^{2}-2t+1)}$=$\frac{4}{t+\frac{1}{t}-2}$,
∵t<0,∴t+$\frac{1}{t}$≤-2,t+$\frac{1}{t}$-2≤-4,
即$\frac{4}{t+\frac{1}{t}-2}$∈[-1,0),
当x≥-$\frac{1}{2}$,ln(x+1)≥ln(-$\frac{1}{2}$+1)=ln$\frac{1}{2}$,
综上f(x)≥-1.
存在实数b使得f(a)+g(b)=0,
则g(b)=-f(a),
则满足g(b)=b2-4b-4≤1,
即b2-4b-5≤0,
解得-1≤b≤5,
故b的取值范围是[-1,5],
故选:D
点评 本题考查的知识点是分段函数,函数的值域,基本不等式,对数函数的性质,存在性问题,二次不等式,是函数和不等式较为综合的应用.

练习册系列答案
相关题目
11.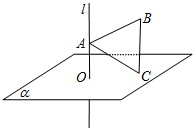 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
 如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )
如图,直线l⊥平面α,垂足为O,已知边长为2的等边三角形ABC在空间做符合以下条件的自由运动:①A∈l,②C∈α,则B,O两点间的最大距离为( )| A. | $1+\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | $1+\sqrt{3}$ | D. | $2+\sqrt{3}$ |
12.有3个学习兴趣小组,甲、乙两位同学各自参加其中一个小组,每位同学参加各个小组的可能性相同,则这两位同学参加同一个兴趣小组的概率为( )
| A. | $\frac{3}{4}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{3}$ |
6. 如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°,设MN=x,BN=n,AM=m,则以x、m、n为边的三角形的形状为( )
如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°,设MN=x,BN=n,AM=m,则以x、m、n为边的三角形的形状为( )
 如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°,设MN=x,BN=n,AM=m,则以x、m、n为边的三角形的形状为( )
如图,等腰直角三角形ABC中,∠ACB=90°,在斜边AB上取两点M、N,使∠MCN=45°,设MN=x,BN=n,AM=m,则以x、m、n为边的三角形的形状为( )| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 随x、m、n的值而定 |
13.定义在R上的偶函数f(x)满足f(x+1)=-f(x),且在[-5,-4]上是减函数,α、β是锐角三角形的两个内角,则( )
| A. | f(sinα)>f(cosβ) | B. | f(sinα)>f(sinβ) | C. | f(sinα)<f(cosβ) | D. | f(cosα)>f(cosβ) |