题目内容
20．已知等差数列{an}，an=$\frac{3}{2}$n-$\frac{21}{2}$，试问：该数列前n项和Sn能否取得最小值？若能，请求出最小值及此时n的值，若不能，请说明理由．分析 由等差数列{an}的通项公式，可得数列{an}中前6项为负值，第7项为0，从第8项开始全为正值．可得数列的前6或7项和最小．
解答 解：由题意等差数列{an}，an=$\frac{3}{2}$n-$\frac{21}{2}$，
令$\frac{3}{2}$n-$\frac{21}{2}$≥0，可得n≥7
故等差数列{an}中前6项为负值，第7项为0，从第8项开始全为正值．
故数列的前6或7项和最小，
点评 本题考查等差数列的通项公式，从数列的变化趋势来求和的最值是解决问题的关键，属基础题．
练习册系列答案
相关题目
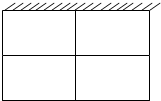如图所示，某畜牧基地要围成相同面积的羊圈4间，一面可利用原有的墙壁，其余各面用篱笆围成，篱笆总长为36m，则每间羊圈的长和宽各为多少时，羊圈面积最大？