题目内容
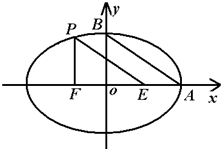 如图,A、B是椭圆
如图,A、B是椭圆| x2 |
| a2 |
| y2 |
| b2 |
分析:由PFE∽△BOA,知
=
,所以a=
c,由此能求出其离心率.
| EF |
| OA |
| PF |
| OB |
| 5 |
解答:解:如图,∵A、B是椭圆
+
=1(a>b>0)的长轴和短轴端点,
点P在椭圆上,F、E是椭圆的左、右焦点,EP∥AB,PF⊥OF,
∴△PFE∽△BOA,
∴
=
,
∴
=
,
∴b2=2bc,b=2c,
∴a2=b2+c2=5c2,a=
c,
∴e=
=
.
故选A.
| x2 |
| a2 |
| y2 |
| b2 |
点P在椭圆上,F、E是椭圆的左、右焦点,EP∥AB,PF⊥OF,
∴△PFE∽△BOA,
∴
| EF |
| OA |
| PF |
| OB |
∴
| 2c |
| a |
| ||
| b |
∴b2=2bc,b=2c,
∴a2=b2+c2=5c2,a=
| 5 |
∴e=
| c |
| a |
| ||
| 5 |
故选A.
点评:本题考查椭圆的性质和应用,解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
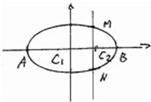 已知如图,A、B是椭圆
已知如图,A、B是椭圆 (2013•惠州模拟)如图,A,B是椭圆
(2013•惠州模拟)如图,A,B是椭圆 如图,A,B是椭圆
如图,A,B是椭圆 如图,A,B是椭圆C:
如图,A,B是椭圆C: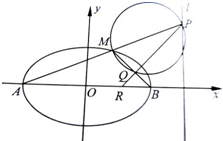 如图,A,B是椭圆
如图,A,B是椭圆