题目内容
函数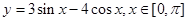 的值域为( )
的值域为( )
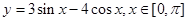 的值域为( )
的值域为( )A. | B. | C.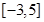 | D. |
B
试题分析:
 ,其中
,其中 ,
, ,且
,且 为锐角,
为锐角, ,
,故当
 时,函数
时,函数 取得最大值
取得最大值 ,且函数
,且函数 在
在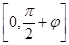 上单调递增,在区间
上单调递增,在区间 上单调递减,故函数
上单调递减,故函数 在
在 或
或 处取得最小值,当
处取得最小值,当 时,
时, ,当
,当 时,
时, ,所以
,所以 ,故函数
,故函数 在区间
在区间 上的值域为
上的值域为 ,故选B.
,故选B.
练习册系列答案
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案
相关题目
题目内容
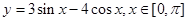 的值域为( )
的值域为( )A. | B. | C.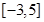 | D. |
 ,其中
,其中 ,
, ,且
,且 为锐角,
为锐角, ,
, 时,函数
时,函数 取得最大值
取得最大值 ,且函数
,且函数 在
在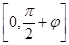 上单调递增,在区间
上单调递增,在区间 上单调递减,故函数
上单调递减,故函数 在
在 或
或 处取得最小值,当
处取得最小值,当 时,
时, ,当
,当 时,
时, ,所以
,所以 ,故函数
,故函数 在区间
在区间 上的值域为
上的值域为 ,故选B.
,故选B.
 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案