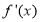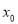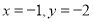题目内容
已知椭圆 的离心率为
的离心率为 ,左右焦点分别为
,左右焦点分别为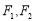 ,且
,且 .
.
(1)求椭圆C的方程;
(2)过点 的直线与椭圆
的直线与椭圆 相交于
相交于 两点,且
两点,且 ,求
,求 的面积.
的面积.
(1)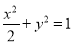 ;(2)
;(2)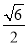
【解析】
试题分析:(1)因为要求椭圆的方程,必须求出两个关于椭圆的三个基本量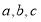 的等式,依题意可得,离心率,焦距的长即可求出相应的
的等式,依题意可得,离心率,焦距的长即可求出相应的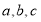 的大小,从而可求出椭圆的方程.
的大小,从而可求出椭圆的方程.
(2)要求三角形的面积通过求出弦长和焦点到直线的距离,从而根据三角形的面积可得三角形的面积.弦长公式的计算需要具备解方程的能力,应用韦达定理,弦长公式,化简等式的能力;运用点到直线的距离公式计算三角形的高.
试题解析:(1)由已知 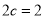 ,所以
,所以 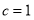 .
.
因为椭圆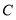 的离心率为
的离心率为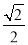 ,所以
,所以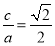 .
.
所以 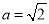 . 所以
. 所以 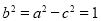 ,
,
故椭圆C的方程为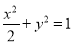 .
.
(2)若直线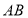 的方程为
的方程为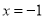 ,则
,则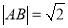 ,不符合题意.
,不符合题意.
设直线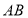 的方程为
的方程为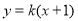 ,
,
由 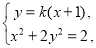 消去y得
消去y得 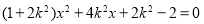 ,
,
显然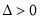 成立,设
成立,设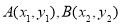 ,
,
则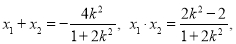
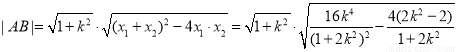
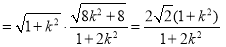 .
.
由已知 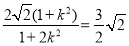 ,解得
,解得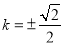 .当
.当 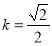 ,直线
,直线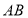 的方程为
的方程为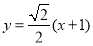 ,即
,即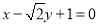 ,
,
点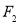 到直线
到直线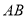 的距离
的距离 .所以
.所以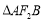 的面
的面
积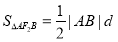
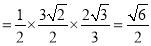 .
.
当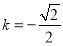 ,
,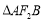 的面积也等于
的面积也等于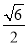 .
.
综上,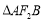 的面积等于
的面积等于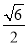 .
.
考点:1.直线与圆的位置关系.2.待定系数求椭圆的方程.3.解方程的能力.4.三角形的面积公式.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案
相关题目