题目内容
平面直角坐标系xOy中，已知A1（x1，y1），A2（x2，y2），…，An（xn，yn）是直线l：y=kx+b上的n个点（n∈N*，k、b均为非零常数）．
（1）若数列{xn}成等差数列，求证：数列{yn}也成等差数列；
（2）若点P是直线l上一点，且
| OP |
| OA1 |
| OA2 |
（3）若点P满足
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
| OP |
| OA1 |
| OA2 |
| OAn |
①系数数列{an}需满足怎样的条件，点P会落在直线l上？
②若点P落在直线l上，系数数列{an}会满足怎样的结论？
③能否根据你给出的系数数列{an}满足的条件，确定在直线l上的点P的个数或坐标？
试提出一个相关命题（或猜想）并开展研究，写出你的研究过程．[本小题将根据你提出的命题（或猜想）的完备程度和研究过程中体现的思维层次，给予不同的评分]．
分析：（1）若设等差数列{xn}的公差为d，易得yn+1-yn为常数，即证数列{yn}是等差数列；
（2）由点P、A1和A2都是直线l上的点，知
=λ
（其中λ≠-1）；由向量的线性运算，得
=
+
=
+λ
=
+λ(
-
)；整理可得
=
+
；即得a1+a2的值；
（3）设存在点P（x，y）满足
=a1
+a2
+…+an
，则x=a1x1+a2x2+…+anxn，当i+j=n+1时，有ai=aj，所以x=anx1+an-1x2+…+a2xn-1+a1xn，则2x=a1（x1+xn）+a2（x2+xn-1）+…+an（xn+x1），由数列{xn}是等差数列，则x1+xn=x2+xn-1=…=xn+x1，可得2x，从而得x，同理得y；即得点P在直线l上．
（2）由点P、A1和A2都是直线l上的点，知
| A1P |
| PA2 |
| OP |
| OA1 |
| A1P |
| OA1 |
| PA2 |
| OA1 |
| OA2 |
| OP |
| OP |
| 1 |
| 1+λ |
| OA1 |
| λ |
| 1+λ |
| OA2 |
（3）设存在点P（x，y）满足
| OP |
| OA1 |
| OA2 |
| OAn |
解答：解：（1）证明：设等差数列{xn}的公差为d，因为yn+1-yn=（kxn+1+b）-（kxn+b）=k（xn+1-xn）=kd是常数，
∴数列{yn}等差数列．
（2）因为点P、A1和A2都是直线l上一点，故有
=λ
（其中λ≠-1）；
于是，
=
+
=
+λ
=
+λ(
-
)；
∴(1+λ)
=
+λ
，即
=
+
；
令a1=
，a2=
，则有a1+a2=1．
（3）假设存在点P（x，y）满足
=a1
+a2
+…+an
，
则有x=a1x1+a2x2+…+anxn，且当i+j=n+1时，恒有ai=aj，
所以有x=anx1+an-1x2+…+a2xn-1+a1xn，
所以2x=a1（x1+xn）+a2（x2+xn-1）+…+an（xn+x1），
又因为数列{xn}成等差数列，于是x1+xn=x2+xn-1=…=xn+x1，
所以，2x=（a1+a2+…+an）（x1+xn）=x1+xn；
故x=
，同理y=
，且点P(
，
)在直线l上（是A1、An的中点），
即存在点P(
，
)满足要求．
∴数列{yn}等差数列．
（2）因为点P、A1和A2都是直线l上一点，故有
| A1P |
| PA2 |
于是，
| OP |
| OA1 |
| A1P |
| OA1 |
| PA2 |
| OA1 |
| OA2 |
| OP |
∴(1+λ)
| OP |
| OA1 |
| OA2 |
| OP |
| 1 |
| 1+λ |
| OA1 |
| λ |
| 1+λ |
| OA2 |
令a1=
| 1 |
| 1+λ |
| λ |
| 1+λ |
（3）假设存在点P（x，y）满足
| OP |
| OA1 |
| OA2 |
| OAn |
则有x=a1x1+a2x2+…+anxn，且当i+j=n+1时，恒有ai=aj，
所以有x=anx1+an-1x2+…+a2xn-1+a1xn，
所以2x=a1（x1+xn）+a2（x2+xn-1）+…+an（xn+x1），
又因为数列{xn}成等差数列，于是x1+xn=x2+xn-1=…=xn+x1，
所以，2x=（a1+a2+…+an）（x1+xn）=x1+xn；
故x=
| x1+xn |
| 2 |
| y1+yn |
| 2 |
| x1+xn |
| 2 |
| y1+yn |
| 2 |
即存在点P(
| x1+xn |
| 2 |
| y1+yn |
| 2 |
点评：本题考查了等差数列以及平面向量知识的综合应用，属于较难的题目；解题时须要认真审题，细心解答，以免出错．
练习册系列答案
相关题目
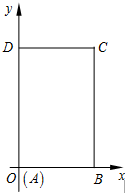如图，在平面直角坐标系xOy中，已知矩形ABCD的两边AB，CD分别落在x轴、y轴的正半轴上，且AB=2，AD=4，点A与坐标原点重合．现将矩形折叠，使点A落在线段DC上，若折痕所在的直线的斜率为k，试写出折痕所在直线的方程及k的范围．