��Ŀ����
ƽ��ֱ������ϵxOy�У���֪A1��x1��y1����A2��x2��y2��������An��xn��yn����ֱ��l��y=kx+b�ϵ�n������n��N*��k��b��Ϊ���㳣������
��1��������{xn}�ɵȲ����У���֤������{yn}Ҳ�ɵȲ����У�
��2������P��ֱ��l��һ�㣬��
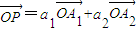 ����a1+a2��ֵ��
����a1+a2��ֵ����3������P����
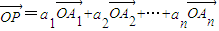 �����dz�
�����dz�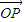 ������
������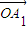 ��
��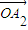 ������
������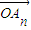 ��������ϣ�{an}�Ǹ�������ϵ�ϵ�����У���
��������ϣ�{an}�Ǹ�������ϵ�ϵ�����У���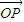 ������
������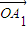 ��
��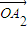 ������
������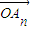 ���������ʱ����ο�����������
���������ʱ����ο�������������ϵ������{an}��������������������P������ֱ��l�ϣ�
������P����ֱ��l�ϣ�ϵ������{an}�����������Ľ��ۣ�
���ܷ�����������ϵ������{an}�����������ȷ����ֱ��l�ϵĵ�P�ĸ��������ꣿ
�����һ��������⣨����룩����չ�о���д������о����̣�[��С�⽫��������������⣨����룩���걸�̶Ⱥ��о����������ֵ�˼ά��Σ����費ͬ������]��
���𰸡���������1������Ȳ�����{xn}�Ĺ���Ϊd����yn+1-ynΪ��������֤����{yn}�ǵȲ����У�
��2���ɵ�P��A1��A2����ֱ��l�ϵĵ㣬֪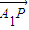 =��
=��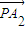 �����Цˡ�-1�������������������㣬��
�����Цˡ�-1�������������������㣬��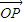 =
=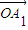 +
+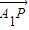 =
=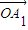 +
+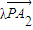 =
=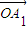 +��
+��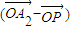 �������ɵ�
�������ɵ�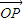 =
=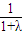
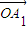 +
+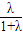
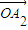 ������a1+a2��ֵ��
������a1+a2��ֵ��
��3������ڵ�P��x��y������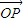 =a1
=a1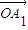 +a2
+a2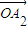 +��+an
+��+an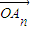 ����x=a1x1+a2x2+��+anxn����i+j=n+1ʱ����ai=aj������x=anx1+an-1x2+��+a2xn-1+a1xn����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����������{xn}�ǵȲ����У���x1+xn=x2+xn-1=��=xn+x1���ɵ�2x���Ӷ���x��ͬ����y�����õ�P��ֱ��l�ϣ�
����x=a1x1+a2x2+��+anxn����i+j=n+1ʱ����ai=aj������x=anx1+an-1x2+��+a2xn-1+a1xn����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����������{xn}�ǵȲ����У���x1+xn=x2+xn-1=��=xn+x1���ɵ�2x���Ӷ���x��ͬ����y�����õ�P��ֱ��l�ϣ�
����⣺��1��֤������Ȳ�����{xn}�Ĺ���Ϊd����Ϊyn+1-yn=��kxn+1+b��-��kxn+b��=k��xn+1-xn��=kd�dz�����
������{yn}�Ȳ����У�
��2����Ϊ��P��A1��A2����ֱ��l��һ�㣬����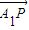 =��
=��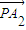 �����Цˡ�-1����
�����Цˡ�-1����
���ǣ�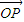 =
=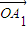 +
+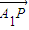 =
=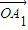 +
+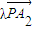 =
=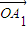 +��
+��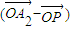 ��
��
��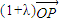 =
=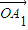 +��
+��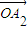 ����
����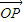 =
=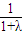
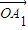 +
+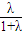
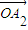 ��
��
��a1=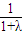 ��a2=
��a2=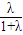 ������a1+a2=1��
������a1+a2=1��
��3��������ڵ�P��x��y������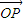 =a1
=a1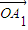 +a2
+a2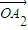 +��+an
+��+an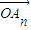 ��
��
����x=a1x1+a2x2+��+anxn���ҵ�i+j=n+1ʱ������ai=aj��
������x=anx1+an-1x2+��+a2xn-1+a1xn��
����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����
����Ϊ����{xn}�ɵȲ����У�����x1+xn=x2+xn-1=��=xn+x1��
���ԣ�2x=��a1+a2+��+an����x1+xn��=x1+xn��
��x=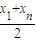 ��ͬ��y=
��ͬ��y=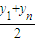 ���ҵ�P
���ҵ�P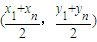 ��ֱ��l�ϣ���A1��An���е㣩��
��ֱ��l�ϣ���A1��An���е㣩��
�����ڵ�P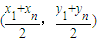 ����Ҫ��
����Ҫ��
���������⿼���˵Ȳ������Լ�ƽ������֪ʶ���ۺ�Ӧ�ã����ڽ��ѵ���Ŀ������ʱ��Ҫ�������⣬ϸ�Ľ�����������
��2���ɵ�P��A1��A2����ֱ��l�ϵĵ㣬֪
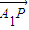 =��
=��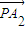 �����Цˡ�-1�������������������㣬��
�����Цˡ�-1�������������������㣬��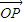 =
=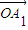 +
+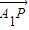 =
=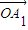 +
+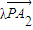 =
=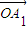 +��
+��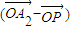 �������ɵ�
�������ɵ�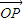 =
=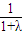
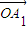 +
+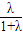
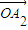 ������a1+a2��ֵ��
������a1+a2��ֵ����3������ڵ�P��x��y������
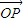 =a1
=a1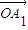 +a2
+a2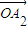 +��+an
+��+an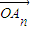 ����x=a1x1+a2x2+��+anxn����i+j=n+1ʱ����ai=aj������x=anx1+an-1x2+��+a2xn-1+a1xn����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����������{xn}�ǵȲ����У���x1+xn=x2+xn-1=��=xn+x1���ɵ�2x���Ӷ���x��ͬ����y�����õ�P��ֱ��l�ϣ�
����x=a1x1+a2x2+��+anxn����i+j=n+1ʱ����ai=aj������x=anx1+an-1x2+��+a2xn-1+a1xn����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����������{xn}�ǵȲ����У���x1+xn=x2+xn-1=��=xn+x1���ɵ�2x���Ӷ���x��ͬ����y�����õ�P��ֱ��l�ϣ�����⣺��1��֤������Ȳ�����{xn}�Ĺ���Ϊd����Ϊyn+1-yn=��kxn+1+b��-��kxn+b��=k��xn+1-xn��=kd�dz�����
������{yn}�Ȳ����У�
��2����Ϊ��P��A1��A2����ֱ��l��һ�㣬����
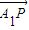 =��
=��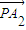 �����Цˡ�-1����
�����Цˡ�-1�������ǣ�
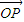 =
=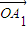 +
+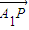 =
=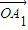 +
+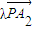 =
=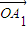 +��
+��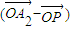 ��
����
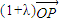 =
=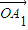 +��
+��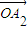 ����
����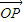 =
=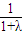
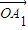 +
+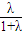
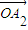 ��
����a1=
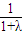 ��a2=
��a2=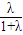 ������a1+a2=1��
������a1+a2=1����3��������ڵ�P��x��y������
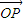 =a1
=a1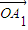 +a2
+a2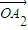 +��+an
+��+an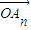 ��
������x=a1x1+a2x2+��+anxn���ҵ�i+j=n+1ʱ������ai=aj��
������x=anx1+an-1x2+��+a2xn-1+a1xn��
����2x=a1��x1+xn��+a2��x2+xn-1��+��+an��xn+x1����
����Ϊ����{xn}�ɵȲ����У�����x1+xn=x2+xn-1=��=xn+x1��
���ԣ�2x=��a1+a2+��+an����x1+xn��=x1+xn��
��x=
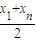 ��ͬ��y=
��ͬ��y=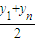 ���ҵ�P
���ҵ�P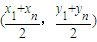 ��ֱ��l�ϣ���A1��An���е㣩��
��ֱ��l�ϣ���A1��An���е㣩�������ڵ�P
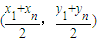 ����Ҫ��
����Ҫ�����������⿼���˵Ȳ������Լ�ƽ������֪ʶ���ۺ�Ӧ�ã����ڽ��ѵ���Ŀ������ʱ��Ҫ�������⣬ϸ�Ľ�����������

��ϰ��ϵ�д�
�����Ŀ
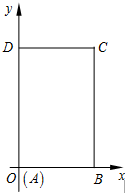 ��ͼ����ƽ��ֱ������ϵxOy�У���֪����ABCD������AB��CD�ֱ�����x�ᡢy����������ϣ���AB=2��AD=4����A������ԭ���غϣ��ֽ������۵���ʹ��A�����߶�DC�ϣ����ۺ����ڵ�ֱ�ߵ�б��Ϊk����д���ۺ�����ֱ�ߵķ��̼�k�ķ�Χ��
��ͼ����ƽ��ֱ������ϵxOy�У���֪����ABCD������AB��CD�ֱ�����x�ᡢy����������ϣ���AB=2��AD=4����A������ԭ���غϣ��ֽ������۵���ʹ��A�����߶�DC�ϣ����ۺ����ڵ�ֱ�ߵ�б��Ϊk����д���ۺ�����ֱ�ߵķ��̼�k�ķ�Χ��