题目内容
在平面直角坐标系
中，设点
为圆
：
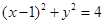上的任意一点，点
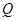(2
，
) (
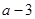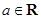)，则线段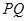
长度的最小值为 ．
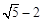
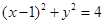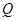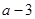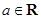解析试题分析：根据题意，由于点为圆：上的任意一点，由于圆心（1,0），且点(2，) ()，则线段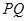长度的最小值为圆心到Q的距离减去圆的半径2，那么可知
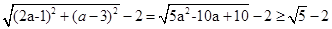，故可知答案为。
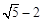考点：两点之间的距离
点评：主要是考查了两点之间的距离的求解的运用，属于基础题。
练习册系列答案
相关题目
题目内容
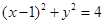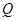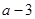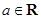在平面直角坐标系中，设点为圆：上的任意一点，点(2，) ()，则线段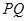长度的最小值为 ．
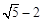
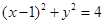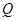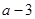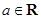解析试题分析：根据题意，由于点为圆：上的任意一点，由于圆心（1,0），且点(2，) ()，则线段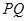长度的最小值为圆心到Q的距离减去圆的半径2，那么可知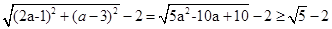，故可知答案为。
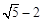考点：两点之间的距离
点评：主要是考查了两点之间的距离的求解的运用，属于基础题。
作一直线与椭圆
相交于A、B两点，若
点恰好为弦
的中点，则
的渐近线与圆
相切，则该双曲线的离心率为_________．
表示椭圆，则
的取值范围是______________. 
的焦点坐标是____________.
（
）与曲线
（
）上任意两点，则|
|最小值为 . 
的抛物线的标准方程是 ．
，则其离心率等于_______________．
，则
．