Question

7．如图，某市三个新兴工业小区A，B，C决定平均投资共同建一个中心医院O，使得医院到三个小区的距离相等，已知这三个小区之间的距离分别为AB=4.3km，BC=3.7km，CA=4.7km，该医院应建在何处（精确到0.1km或1°）？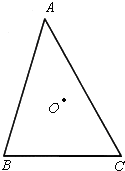

Answer 1

分析 由余弦定理求出cosA，可得sinA，利用正弦定理，即可得出结论．

解答 解：由余弦定理有cosA=$\frac{4．{3}^{2}+4．{7}^{2}-3．{7}^{2}}{2×4.3×4.7}$=0.6653，
∴sinA=0.7466，
由正弦定理：$\frac{3.7}{sinA}$=2R，∴R=$\frac{3.7}{2×0.7466}$=2.5km．
故医院应建在离A，B，C距离均为2.5 km处．

点评 本题考查利用数学知识解决实际问题，考查余弦定理、正弦定理的运用，属于中档题．