题目内容
下列命题:
①命题“若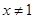 ,则
,则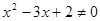 ”的逆否命题: “若
”的逆否命题: “若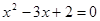 ,则
,则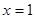 ”.
”.
②命题 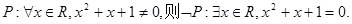
③“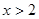 ”是“
”是“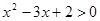 ”的充分不必要条件.
”的充分不必要条件.
④若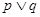 为真命题,则
为真命题,则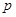 ,
,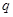 均为真命题.
均为真命题.
其中真命题的个数有
| A.4个 | B.3个 |
| C.2个 | D.1个 |
B
解析试题分析:因为求解一个命题的逆否命题就是将原命题中的结论的否定作为条件,条件的豆丁作为结论得到的新命题即①命题“若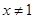 ,则
,则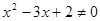 ”的逆否命题: “若
”的逆否命题: “若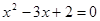 ,则
,则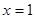 ”.成立。
”.成立。
②中对于全称命题的否定,就是将任意改为存在,命题的结论改为否定,即得到命题 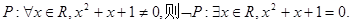 成立
成立
③中条件是“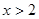 ”结论根据一元二次不等式解得为“
”结论根据一元二次不等式解得为“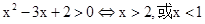 ”利用集合的思想可知小集合是大集合的充分不必要条件,故成立。.
”利用集合的思想可知小集合是大集合的充分不必要条件,故成立。.
④中或命题为真,说明p,q至少有一个为真,那么题目中都是为真,因此是错误。因此可知真命题的个数为3个,选B.
考点:本试题主要是考查了命题的真假和四种命题的关系的运用,以及充分条件的判定问题。
点评:解决该试题的关键是对于命题中逻辑联结词概念的理解,以及命题的否定的运用。

练习册系列答案
相关题目
命题“?x>0,x2+x>0”的否定是( ).
A.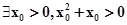 | B.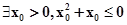 |
| C.?x>0,x2+x≤0 | D.?x≤0,x2+x>0 |
下列有关命题的说法正确的是
A.命题“若 ,则 ,则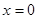 ”的否命题为:“若 ”的否命题为:“若 ,则 ,则 ” ” |
B.“若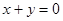 ,则 ,则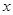 , ,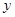 互为相反数”的逆命题为真命题 互为相反数”的逆命题为真命题 |
C.命题“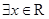 ,使得 ,使得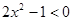 ”的否定是:“ ”的否定是:“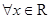 ,均有 ,均有 ” ” |
D.命题“若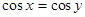 ,则 ,则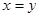 ”的逆否命题为真命题 ”的逆否命题为真命题 |
下列说法中,正确的是
A.命题“若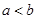 ,则 ,则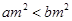 ”的否命题是假命题. ”的否命题是假命题. |
B.设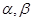 为两个不同的平面,直线 为两个不同的平面,直线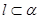 ,则 ,则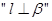 是 是 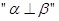 成立的充分不必要条件. 成立的充分不必要条件. |
C.命题“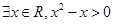 ”的否定是“ ”的否定是“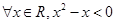 ”. ”. |
D.已知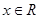 ,则“ ,则“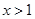 ”是“ ”是“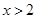 ”的充分不必要条件. ”的充分不必要条件. |
若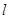 为一条直线,
为一条直线,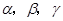 为三个互不重合的平面,给出下面三个命题:
为三个互不重合的平面,给出下面三个命题:
①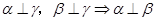 ;②
;②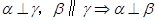 ;③
;③ .其中正确的命题有( )
.其中正确的命题有( )
| A.0个 | B.1个 | C.2个 | D.3个 |
给出下列命题:(1)等比数列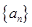 的公比为
的公比为 ,则“
,则“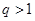 ”是“
”是“ ”的既不充分也不必要条件;(2)“
”的既不充分也不必要条件;(2)“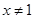 ”是“
”是“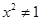 ”的必要不充分条件;(3)函数的
”的必要不充分条件;(3)函数的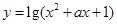 的值域为R,则实数
的值域为R,则实数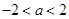 ;(4)“
;(4)“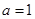 ”是“函数
”是“函数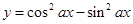 的最小正周期为
的最小正周期为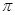 ”的充要条件.其中真命题的个数是
”的充要条件.其中真命题的个数是
| A.1 | B.2 | C.3 | D.4 |
已知向量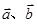 都是非零向量,“
都是非零向量,“ ”是“
”是“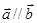 ”的( )
”的( )
| A.必要非充分条件. | B.充分非必要条件. |
| C.充要条件. | D.既非充分也非必要条件 |
不等式 的解集非空的一个必要而不充分条件是( )
的解集非空的一个必要而不充分条件是( )
A.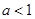 | B.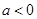 | C.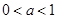 | D.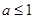 |
 是幂函数,则函数
是幂函数,则函数