题目内容
【题目】设a∈R，若x＞0时均有[（a﹣1）x﹣1]（x2﹣ax﹣1）≥0，则a= ．
【答案】
【解析】解：（1）a=1时，代入题中不等式明显不成立．（2）a≠1，构造函数y1=（a﹣1）x﹣1，y2=x 2﹣ax﹣1，它们都过定点P（0，﹣1）．考查函数y1=（a﹣1）x﹣1：令y=0，得M（ 
，0），∴a＞1；考查函数y2=x2﹣ax﹣1，∵x＞0时均有[（a﹣1）x﹣1]（x2﹣ax﹣1）≥0，∴y2=x2﹣ax﹣1过点M（ ，0），代入得： 
，解之得：a= ，或a=0（舍去）．故答案为： ．
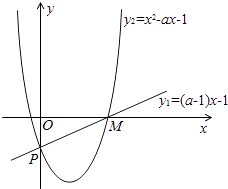
分类讨论，（1）a=1；（2）a≠1，在x＞0的整个区间上，我们可以将其分成两个区间，在各自的区间内恒正或恒负，即可得到结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
