题目内容
【题目】已知点A(0,﹣2),椭圆E: ![]() 的离心率为
的离心率为 ![]() ,F是椭圆E的右焦点,直线AF的斜率为
,F是椭圆E的右焦点,直线AF的斜率为 ![]() ,O为坐标原点.
,O为坐标原点.
(1)求椭圆E的方程;
(2)设过点A的动直线与椭圆E相交于P,Q两点,当△OPQ的面积最大时,求直线l的方程.
【答案】
(1)解:设F(c,0), ![]() ,解得
,解得 ![]() ,又
,又 ![]() ,∴a=2,b=1,
,∴a=2,b=1,
∴椭圆E: ![]() ;
;
(2)解:当l⊥x轴时,不合题意;
当直线l斜率存在时,设直线l:y=kx﹣2,P(x1,y1),Q(x2,y2),
联立 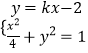 ,得(1+4k2)x2﹣16kx+12=0.
,得(1+4k2)x2﹣16kx+12=0.
由△=16(4k2﹣3)>0,得 ![]() ,即
,即 ![]() 或k
或k ![]() .
.
![]() ,
,
从而 ![]()
= ![]() ,
,
又点O到直线PQ的距离 ![]() ,
,
∴△OPQ的面积 ![]() ,
,
设 ![]() ,则t>0,
,则t>0,
∴ ![]() ,当且仅当t=2,
,当且仅当t=2,
即 ![]() 时,等号成立,且△>0.
时,等号成立,且△>0.
此时 ![]() .
.
【解析】(1)设出F,由直线AF的斜率为 ![]() 求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;(2)当l⊥x轴时,不合题意;当直线l斜率存在时,设直线l:y=kx﹣2,联立直线方程和椭圆方程,由判别式大于0求得k的范围,再由弦长公式求得|PQ|,由点到直线的距离公式求得O到l的距离,代入三角形面积公式,化简后换元,利用基本不等式求得最值,进一步求出k值,则直线方程可求.
求得c,结合离心率求得a,再由隐含条件求得b,则椭圆方程可求;(2)当l⊥x轴时,不合题意;当直线l斜率存在时,设直线l:y=kx﹣2,联立直线方程和椭圆方程,由判别式大于0求得k的范围,再由弦长公式求得|PQ|,由点到直线的距离公式求得O到l的距离,代入三角形面积公式,化简后换元,利用基本不等式求得最值,进一步求出k值,则直线方程可求.

练习册系列答案
相关题目
【题目】从某高中随机选取5名高一男生,其身高和体重的数据如表所示:
身高x(cm) | 160 | 165 | 170 | 175 | 180 |
体重y(kg) | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 ![]() =0.56x+
=0.56x+ ![]() ,据此模型可预报身高为172cm的高一男生的体重为( )
,据此模型可预报身高为172cm的高一男生的体重为( )
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg