题目内容
【题目】已知圆O：x2+y2=4与x轴相交于A，B两点，圆内的动点P使|PA|、|PO|、|PB|成等比数列，求 
的取值范围．
【答案】解：不妨设A（x1 ， 0），B（x2 ， 0），x1＜x2 ． 由x2=4即得A（﹣2，0），B（2，0）．
设P（x，y），由|PA|，|PO|，|PB|成等比数列，得 
，
两边平方，可得（x2+y2+4）2﹣16x2=（x2+y2）2 ，
化简整理可得，x2﹣y2=2．
=（﹣2﹣x，﹣y）（2﹣x，﹣y）=x2﹣4+y2=2（y2﹣1）．
由于点P在圆O内，故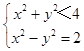 
，
由此得y2＜1．
所以 的取值范围为[﹣2，0）．
【解析】根据圆内的动点P使|PA|、|PO|、|PB|成等比数列，列出方程，再根据点P在圆内求出取值范围．
练习册系列答案
相关题目
【题目】从某高中随机选取5名高一男生，其身高和体重的数据如表所示：
身高x（cm） | 160 | 165 | 170 | 175 | 180 |
体重y（kg） | 63 | 66 | 70 | 72 | 74 |
根据如表可得回归方程 
=0.56x+ 
，据此模型可预报身高为172cm的高一男生的体重为（ ）
A.70.12kg
B.70.29kg
C.70.55kg
D.71.05kg
