题目内容
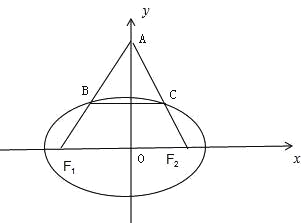
【题目】椭圆b2x2+a2y2=a2b2(a>b>0)的两个焦点分别是F1、F2,等边三角形的边AF1、AF2与该椭圆分别相交于B、C两点,且2|BC|=|F1F2|,则该椭圆的离心率等于( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】C
【解析】
由△AF1F2为正三角形可得∠AF1F2=∠A=60°,则可求直线AF1,AF2的斜率,进而可求B点坐标,代入椭圆的方程,结合b2=a2﹣c2及0<e<1可求离心率.
由△AF1F2为正三角形可得∠AF1F2=∠AF2F1=60°
则直线AF1,AF2的斜率分别为 ![]() ,
,![]()
则直线AF1,AF2所在的直线方程分别为y![]() ,y
,y![]() ,
,
其交点A(0,![]() c),由于2|BC|=|F1F2|,得BC是三角形的中位线,得B是AF1的中点,
c),由于2|BC|=|F1F2|,得BC是三角形的中位线,得B是AF1的中点,
从而AF1中点B( ![]() ,
,![]() )在椭圆上,代入椭圆的方程可得
)在椭圆上,代入椭圆的方程可得 ![]()
整理可得,c2(a2﹣c2)+3c2a2=4a2(a2﹣c2)
∴4a4﹣8a2c2+c4=0
两边同时除以a4可得,e4﹣8e2+4=0
∵0<e<1
∴![]() ,
,![]() (舍)
(舍)
∴![]()
故选:C.

 轻松暑假总复习系列答案
轻松暑假总复习系列答案【题目】苹果是人们日常生活中常见的营养型水果.某地水果批发市场销售来自5个不同产地的富士苹果,各产地的包装规格相同,它们的批发价格(元/箱)和市场份额如下:
产地 |
|
|
|
|
|
批发价格 |
|
|
|
|
|
市场份额 |
|
|
|
|
|
市场份额亦称“市场占有率”.指某一产品的销售量在市场同类产品中所占比重.
(1)从该地批发市场销售的富士苹果中随机抽取一箱,求该箱苹果价格低于![]() 元的概率;
元的概率;
(2)按市场份额进行分层抽样,随机抽取![]() 箱富士苹果进行检验,
箱富士苹果进行检验,
①从产地![]() 共抽取
共抽取![]() 箱,求
箱,求![]() 的值;
的值;
②从这![]() 箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
箱苹果中随机抽取两箱进行等级检验,求两箱产地不同的概率;
(3)由于受种植规模和苹果品质的影响,预计明年产地![]() 的市场份额将增加
的市场份额将增加![]() ,产地
,产地![]() 的市场份额将减少
的市场份额将减少![]() ,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱
,其它产地的市场份额不变,苹果销售价格也不变(不考虑其它因素).设今年苹果的平均批发价为每箱![]() 元,明年苹果的平均批发价为每箱
元,明年苹果的平均批发价为每箱![]() 元,比较
元,比较![]() 的大小.(只需写出结论)
的大小.(只需写出结论)