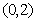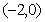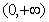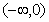题目内容
(本题满分13分)已知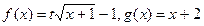 ,(
,(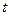 为参数) (1)当
为参数) (1)当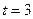 时,解不等式
时,解不等式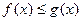 (2)如果当
(2)如果当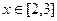 时,
时,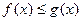 恒成立,求
恒成立,求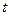 的取值范围。
的取值范围。
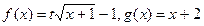 ,(
,(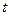 为参数) (1)当
为参数) (1)当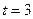 时,解不等式
时,解不等式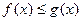 (2)如果当
(2)如果当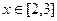 时,
时,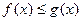 恒成立,求
恒成立,求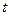 的取值范围。
的取值范围。(Ⅰ)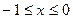 或
或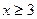 (Ⅱ)
(Ⅱ) 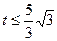
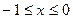 或
或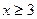 (Ⅱ)
(Ⅱ) 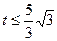
(1)当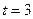 时,
时,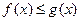 即:
即: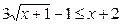
∴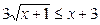 等价于:
等价于: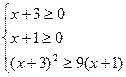
解之得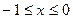 或
或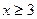 (6分)
(6分)
(2)当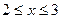 时,
时,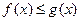 恒成立即不等式:
恒成立即不等式: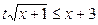 在
在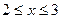 时恒成立
时恒成立
即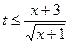 在
在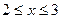 时恒成立(9分)
时恒成立(9分)
令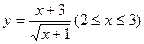 ,则有
,则有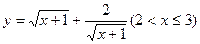
令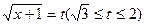 ,∴
,∴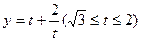
由于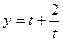 在
在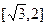 上为增函数,∴
上为增函数,∴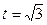 即
即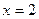 时,
时,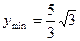
∴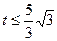 (13分)
(13分)
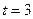 时,
时,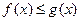 即:
即: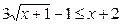
∴
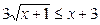 等价于:
等价于: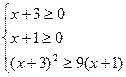
解之得
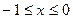 或
或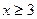 (6分)
(6分)(2)当
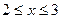 时,
时,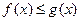 恒成立即不等式:
恒成立即不等式: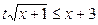 在
在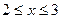 时恒成立
时恒成立即
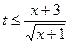 在
在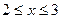 时恒成立(9分)
时恒成立(9分)令
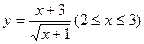 ,则有
,则有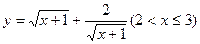
令
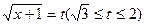 ,∴
,∴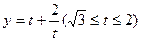
由于
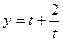 在
在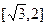 上为增函数,∴
上为增函数,∴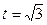 即
即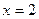 时,
时,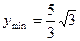
∴
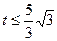 (13分)
(13分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
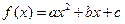 对于
对于 1、
1、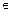 R,且
R,且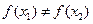 ,求证:方程
,求证:方程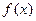 =
=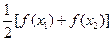 有不等实根,且必有一根属于区间(
有不等实根,且必有一根属于区间(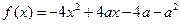 在区间
在区间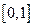 内有一最大值
内有一最大值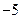 ,求
,求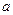 的值.
的值.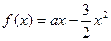 的最大值不大于
的最大值不大于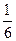 ,又当
,又当 ,求
,求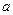 的值。
的值。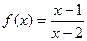 .
.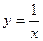 的图象平移
的图象平移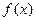 的图象,并写出交换过程;
的图象,并写出交换过程;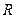 上的函数
上的函数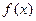 既是奇函数又是周期函数,若
既是奇函数又是周期函数,若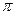 ,且当x∈[0,
,且当x∈[0,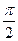 )时,
)时, ,则
,则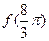 的值为 ( )
的值为 ( )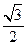
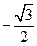
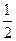

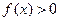 ,则下列一定成立的是( )
,则下列一定成立的是( )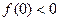
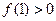
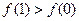
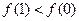
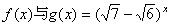 图象关于
图象关于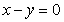 对称,则
对称,则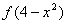 的增区间为( )
的增区间为( )