题目内容
在空间四边形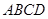 中,
中,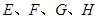 分别是
分别是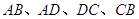 的中点,当对角线
的中点,当对角线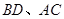 满足 时,四边形
满足 时,四边形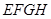 的形状是菱形.
的形状是菱形.

解析试题分析:根据题意,由于在空间四边形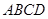 中,
中,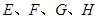 分别是
分别是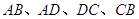 的中点,则利用中位线的性质可知,四边形为平行四边形,那么可知,要成为菱形,则邻边要相等,故可知,只有
的中点,则利用中位线的性质可知,四边形为平行四边形,那么可知,要成为菱形,则邻边要相等,故可知,只有 时可知成立故答案为
时可知成立故答案为
考点:平行四边形的判定
点评:主要是考查了平行的判定以及四边形的形状的确定,属于基础题。

练习册系列答案
相关题目
题目内容
在空间四边形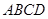 中,
中,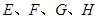 分别是
分别是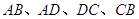 的中点,当对角线
的中点,当对角线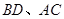 满足 时,四边形
满足 时,四边形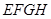 的形状是菱形.
的形状是菱形.

解析试题分析:根据题意,由于在空间四边形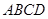 中,
中,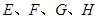 分别是
分别是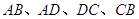 的中点,则利用中位线的性质可知,四边形为平行四边形,那么可知,要成为菱形,则邻边要相等,故可知,只有
的中点,则利用中位线的性质可知,四边形为平行四边形,那么可知,要成为菱形,则邻边要相等,故可知,只有 时可知成立故答案为
时可知成立故答案为
考点:平行四边形的判定
点评:主要是考查了平行的判定以及四边形的形状的确定,属于基础题。
