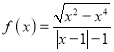Question

【题目】已知定义在R上的奇函数f（x），当x≥0时，f（x）＝x2﹣x．

（1）求函数f（x）的解析式；

（2）若函数g（x）（x≠0），求证：函数g（x）在（0，+∞）单调递增．

Answer 1

【答案】（1）f（x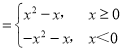）．（2）证明见解析

【解析】

（1）设x＜0，则﹣x＞0，则f（﹣x）＝x2+x，利用函数的奇偶性即可求解.

（2）根据函数单调性定义即可证明.

（1）若x＜0，则﹣x＞0，

则f（﹣x）＝x2+x，

∵f（x）是奇函数，∴f（﹣x）＝x2+x＝﹣f（x），

即f（x）＝﹣x2﹣x，

即f（x）．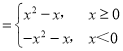

（2）证明：当x＞0时，g（x）x﹣1，

设0＜x1＜x2，

则g（x1）﹣g（x2）＝x1x2（x1﹣x2）（1），

∵0＜x1＜x2，

∴x1﹣x2＜0，x1x2＞0，

则g（x1）﹣g（x2）＜0，即g（x1）＜g（x2），

则函数g（x）在（0，+∞）为增函数．