Question

【题目】已知定义在上的函数满足：对任意都有.

（1）求证：函数是奇函数；

（2）如果当时，有，试判断在上的单调性，并用定义证明你的判断；

（3）在（2）的条件下，若对满足不等式的任意恒成立，求的取值范围.

Answer 1

【答案】（1）证明见解析（2）函数在上为增函数，证明见解析（3）

【解析】

（1）先分析定义域是否关于原点对称，再赋值求，令即可求证（2）先判断在上为增函数，再根据定义证明在上是奇函数，根据奇函数性质知在上为增函数（3）根据（2）可得不等式的解，在此范围恒成立，分离参数即可求解.

（1）函数的定义域关于原点对称，令，可得，

所以，令，则，即，所以函数为奇函数.

（2）函数在上为增函数.

证明如下：

设且，则

，

因为时，有，

所以，

故

即，

所以函数在上是增函数，

根据奇函数的性质知函数在上是增函数，

故在上为增函数.

（3）因为，

所以，

因为在上为增函数，

所以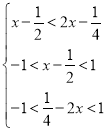，解得.

即当时，恒成立，

所以在上恒成立，

而，

所以只需，

故的取值范围为.