题目内容
9. 如图1是边长为4的等边三角形,将其剪拼成一个正三棱柱模型(如图2),使它的全面积与原三角形的面积相等.D为AC上一点,且BD⊥DC1.
如图1是边长为4的等边三角形,将其剪拼成一个正三棱柱模型(如图2),使它的全面积与原三角形的面积相等.D为AC上一点,且BD⊥DC1.(1)求证:直线AB1∥平面BDC1
(2)求点A到平面BDC1的距离.
分析 (1)根据题目条件得出BD⊥平面AA1C1C,BD⊥AC,D为AC中点,确定条件$\left\{\begin{array}{l}{OD∥A{B}_{1}}\\{OD?平面BD{C}_{1}}\\{A{B}_{1}不在平面}\end{array}\right.$,即AB1∥平面BDC1.
(2)根据条件得出:d等于点C到平面BDC1的距离,CE是点C到平面BDC1的距离,根据CE=$\frac{DC•C{C}_{1}}{D{C}_{1}}$求解即可.
解答 解:(1)证明:连接B1C与BC1交于点O,连接OD,
∵$\left\{\begin{array}{l}{BD⊥D{C}_{1}}\\{BD⊥C{C}_{1}}\\{D{C}_{1}∩C{C}_{1}={C}_{1}}\end{array}\right.$,
∴BD⊥平面AA1C1C,
∴BD⊥AC,
又∵△ABC为等边三角形,
∴AB=BC,
∴D为AC中点,
∵平行四边形BB1C1C中O是B1C的中点,
∴$\left\{\begin{array}{l}{OD∥A{B}_{1}}\\{OD?平面BD{C}_{1}}\\{A{B}_{1}不在平面}\end{array}\right.$,
即AB1∥平面BDC1
(2)设点A到平面BDC1的距离为d
又∵AD=CD,
∴d等于点C到平面BDC1的距离,
过点C作CE⊥DC1垂足为E,
∵DB⊥平面AA1C1C,
∴BD⊥CE,
又∵DB∩DC1=D,∴CE⊥平面DBC1,
则CE是点C到平面BDC1的距离,
∵AC=2,∴CD=1,CC1=$\frac{\sqrt{3}}{3}$,
∴C1D=$\frac{2\sqrt{3}}{3}$,
∴d=CE=$\frac{DC•C{C}_{1}}{D{C}_{1}}$=$\frac{1×\frac{\sqrt{3}}{3}}{\frac{2\sqrt{3}}{3}}$=$\frac{1}{2}$.
点评 本题考查了空间直线平面的平行的判定 定理,空间点性质平面的距离问题,关键是确定距离,转化为平面问题求解,思路要清晰,计算认真.

 名校课堂系列答案
名校课堂系列答案(1)“2a>2b”是“lna>lnb”的充要条件.
(2)命题“正方形是矩形”的否定是“正方形不是矩形”.
(3)“直线a∥直线b”的充分不必要条件是“直线a平行于直线b所在的平面”.
(4)命题“若x≤$\frac{4}{3}$,则$\frac{1}{x-1}$≥3”的逆命题是真命题.
其中正确命题的序号是( )
| A. | (1)(2) | B. | (1)(3) | C. | (4) | D. | (2)(4) |
| A. | a>b>c | B. | a>c>b | C. | b>c>a | D. | b>a>c |
 的定义域为
的定义域为 ,以下命题正确的是( )
,以下命题正确的是( ) 与函数
与函数 的图象关于直线
的图象关于直线 对称;
对称; 的图象既关于点
的图象既关于点 成中心对称,对于任意
成中心对称,对于任意 ,又有
,又有 ,则
,则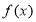 的图象关于直线
的图象关于直线 对称;
对称; ,满足关系式
,满足关系式 ,则函数
,则函数 是奇函数.
是奇函数.