题目内容
17．已知${C}_{n+3}^{n+1}$=${C}_{n+1}^{n-1}$+${C}_{n+1}^{n}$+${C}_{n}^{n-2}$，求n的值．分析 根据组合数的公式，化简${C}_{n+3}^{n+1}$=${C}_{n+1}^{n-1}$+${C}_{n+1}^{n}$+${C}_{n}^{n-2}$，求n的值即可．
解答 解：∵${C}_{n+3}^{n+1}$=${C}_{n+1}^{n-1}$+${C}_{n+1}^{n}$+${C}_{n}^{n-2}$，
即${C}_{n+3}^{2}$=${C}_{n+1}^{2}$+${C}_{n+1}^{1}$+${C}_{n}^{2}$；
∴$\frac{（n+3）（n+2）}{2}$=$\frac{n（n+1）}{2}$+（n+1）+$\frac{n（n-1）}{2}$，
整理，得n2-3n-4=0；
解得n=4或n=-1（舍去），
∴n的值是4．
点评 本题考查了组合数公式的应用问题，是基础题目．
练习册系列答案
相关题目
9．已知数列{an}为等比数列，若a4+a6=10，则a7（a1+2a3）+a3a9的值为（ ）
| A． | 10 | B． | 20 | C． | 100 | D． | 200 |
2．从标有1，2，3，4，5，6的6张纸片中任取2张，那么这2张纸片数字之积为6的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{15}$ | C． | $\frac{2}{15}$ | D． | $\frac{1}{3}$ |
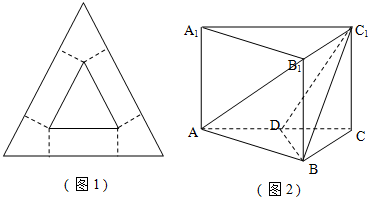如图1是边长为4的等边三角形，将其剪拼成一个正三棱柱模型（如图2），使它的全面积与原三角形的面积相等．D为AC上一点，且BD⊥DC1．