题目内容
(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒.当你到达路口时,求不是红灯的概率.
(2)已知关于x的一元二次函数 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 ,求函数
,求函数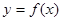 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.
(2)已知关于x的一元二次函数
 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为 和
和 ,求函数
,求函数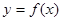 在区间[
在区间[ 上是增函数的概率.
上是增函数的概率.(1)3/5 (2)

(1)本小题可利用对立事件求概率,不是红灯的概率等于1减去是红灯的概率.
(2)解本题的关键是知道f(x)在 是增函数,当且仅当
是增函数,当且仅当
(1)基本事件是遇到红灯、黄灯和绿灯,它们的时间分别为30秒、5秒和40秒,设它们的概率的分别为P1,P2,P3,
所以不是红灯的概率P="1-" P1=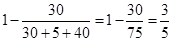
(2)∵函数 的图象的对称轴为
的图象的对称轴为
要使 在区间
在区间 上为增函数,
上为增函数,
当且仅当 >0且
>0且
若 =1则
=1则 =-1,
=-1,
若 =2则
=2则 =-1,1;
=-1,1;
若 =3则
=3则 =-1,1;
=-1,1;
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
(2)解本题的关键是知道f(x)在
 是增函数,当且仅当
是增函数,当且仅当
(1)基本事件是遇到红灯、黄灯和绿灯,它们的时间分别为30秒、5秒和40秒,设它们的概率的分别为P1,P2,P3,
所以不是红灯的概率P="1-" P1=
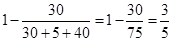
(2)∵函数
 的图象的对称轴为
的图象的对称轴为
要使
 在区间
在区间 上为增函数,
上为增函数,当且仅当
 >0且
>0且
若
 =1则
=1则 =-1,
=-1,若
 =2则
=2则 =-1,1;
=-1,1;若
 =3则
=3则 =-1,1;
=-1,1; ∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为


练习册系列答案
相关题目
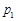 和
和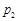 ,则甲、乙至少有1人解答正确的概率是
,则甲、乙至少有1人解答正确的概率是
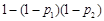


 .
.


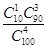




 的
的 个小正方形(如右图),需满足任意相邻(有公共边的)小正方形所涂颜色都不相同,且标号为“
个小正方形(如右图),需满足任意相邻(有公共边的)小正方形所涂颜色都不相同,且标号为“ 、
、 、
、




