题目内容
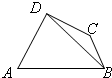如图，在四边形ABCD中，已知AD⊥CD，AD=10，AB=14，∠ADB=60°，BC=8| 2 |
（1）求BD的长（2）若角C为钝角，求角C的度数．
分析：（1）设BD=x，△ABD中由余弦定理可得，AB2=AD2+BD2-2AD•BD•COS∠ADB，可求x
（2）在△BDC中，由正弦定理可得
=
，可求sinC，结合∠C为钝角可求
（2）在△BDC中，由正弦定理可得
| BC |
| sin∠BDC |
| BD |
| sin∠C |
解答：解：（1）设BD=x，△ABD中由余弦定理可得，AB2=AD2+BD2-2AD•BD•COS∠ADB，
即142=102+x2-2×10×x×
，得（x-16）（x+6）=0，负舍，
取x=16，即BD长为16．
（2）∠BDC=30°，在△BDC中，由正弦定理可得
=
，
sinC=
即sin∠C=
，又∠C为钝角，
∴∠C=
即142=102+x2-2×10×x×
| 1 |
| 2 |
取x=16，即BD长为16．
（2）∠BDC=30°，在△BDC中，由正弦定理可得
| BC |
| sin∠BDC |
| BD |
| sin∠C |
sinC=
| 16×sin30° | ||
8
|
| ||
| 2 |
∴∠C=
| 3π |
| 4 |
点评：本题主要考查了正弦定理及余弦定理在解三角形中的应用，解题的关键是熟练掌握基本公式并能灵活应用．
练习册系列答案
相关题目
如图，在四边形ABCD中，△ABC为边长等于
如图，在四边形ABCD中，AC平分∠DAB，∠ABC=60°，AC=7，AD=6，S△ADC=
如图，在四边形ABCD中，AC平分∠DAB，∠ABC=60°，AC=6，AD=5，S△ADC=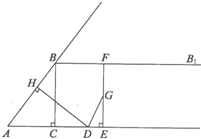
如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，过点B作射线BBl∥AC．动点D从点A出发沿射线AC方向以每秒5个单位的速度运动，同时动点E从点C出发沿射线AC方向以每秒3个单位的速度运动．过点D作DH⊥AB于H，过点E作EF⊥AC交射线BB1于F，G是EF中点，连接DG．设点D运动的时间为t秒．
（2012•青岛二模）如图，在多面体ABC-A1B1C1中，四边形ABB1A1是正方形，AC=AB=1，A1C=A1B，B1C1∥BC，