Question

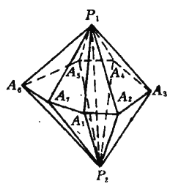
【题目】给定两个七棱锥，它们有公共面的底面，顶点、在底面的两则.现将下述线段中的每一条染红、蓝两色之一:，底面上的所有对角线和所有的侧棱.求证：图中心存在一个同色三角形.

Answer 1

【答案】见解析

【解析】

先证明一个引理：

引理 若同侧的7条侧棱中有5条同色，则命题成立.

证明：在所述条件下，必有两两不相邻的三条侧棱，，同侧，不妨设同为红色，则在三条对角线，，中，若有一条是红色，则有一个红色三角形；若三条都为蓝色，则本身即为单色三角形，引理得证.

现在回到原题.

不妨设.染红色.考虑所有的有序对（的颜色，的颜色）（），其必为（红，红），（红，蓝），（蓝，红），（蓝，蓝）之一.

若某个为（红，红），则为单色三角形.

若无某个为（红，红），则由抽屉原则，存在，使得.分两种情况：

（1）若它们为（红，蓝）或（蓝，红），则易出，，中必有两点不相邻（设为和）知，无论染何种颜色，图中都有一个单色三角形.

（2）为了避免发生（1）的情况，只能（红，蓝）（蓝，红），于是由，引出异于的蓝边都为5条，由引理知命题成立.