题目内容
已知定圆 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆
心 的轨迹为
的轨迹为 .
.
(Ⅰ)求曲线 的方程;
的方程;
(Ⅱ)若点 为曲线
为曲线 上任意一点,证明直线
上任意一点,证明直线 与曲线
与曲线 恒有且只有一个公共点.
恒有且只有一个公共点.
 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆心
 的轨迹为
的轨迹为 .
.(Ⅰ)求曲线
 的方程;
的方程;(Ⅱ)若点
 为曲线
为曲线 上任意一点,证明直线
上任意一点,证明直线 与曲线
与曲线 恒有且只有一个公共点.
恒有且只有一个公共点.解:(Ⅰ)由题知圆 圆心为
圆心为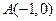 ,半径为
,半径为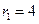 ,设动圆
,设动圆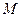 的圆心为
的圆心为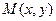
半径为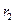 ,
,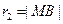 ,由
,由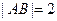 ,可知点
,可知点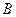 在圆
在圆 内,所以点
内,所以点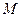 的轨迹是以
的轨迹是以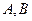 为焦点
为焦点
的椭圆,设椭圆的方程为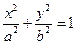
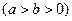 ,由
,由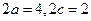 ,得
,得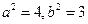 ,
,
故曲线 的方程为
的方程为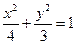 ………………………6分
………………………6分
(Ⅱ)当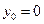 时,由
时,由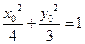 可得
可得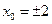
当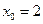 ,
,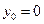 时,直线
时,直线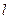 的方程为
的方程为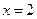 ,直线
,直线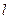 与曲线
与曲线 有且只有一个交点
有且只有一个交点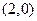 ;
;
当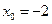 ,
,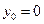 时,直线
时,直线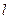 的方程为
的方程为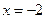 ,直线
,直线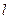 与曲线
与曲线 有且只有一个交点
有且只有一个交点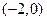 .
.
当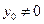 时得
时得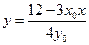 ,代入
,代入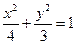 ,消去
,消去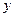 整理得:
整理得:
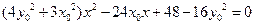 --------------------------------① ………………9分
--------------------------------① ………………9分
由点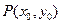 为曲线
为曲线 上一点,故
上一点,故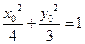 .即
.即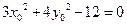
于是方程①可以化简为: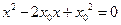
解得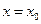 .将
.将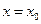 代入
代入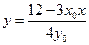 得
得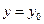 ,说明直线与曲线有且只有一个交点
,说明直线与曲线有且只有一个交点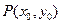 .
.
综上,不论点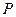 在何位置,直线
在何位置,直线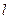 :
: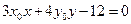 与曲线
与曲线 恒有且只有一个交点,交点即
恒有且只有一个交点,交点即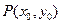 . ……………………………………………12分
. ……………………………………………12分
 圆心为
圆心为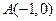 ,半径为
,半径为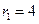 ,设动圆
,设动圆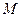 的圆心为
的圆心为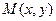
半径为
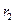 ,
,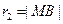 ,由
,由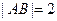 ,可知点
,可知点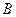 在圆
在圆 内,所以点
内,所以点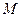 的轨迹是以
的轨迹是以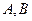 为焦点
为焦点的椭圆,设椭圆的方程为
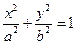
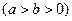 ,由
,由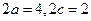 ,得
,得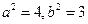 ,
,故曲线
 的方程为
的方程为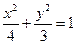 ………………………6分
………………………6分(Ⅱ)当
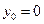 时,由
时,由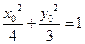 可得
可得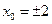
当
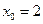 ,
,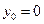 时,直线
时,直线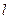 的方程为
的方程为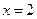 ,直线
,直线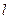 与曲线
与曲线 有且只有一个交点
有且只有一个交点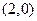 ;
;当
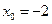 ,
,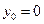 时,直线
时,直线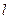 的方程为
的方程为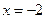 ,直线
,直线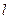 与曲线
与曲线 有且只有一个交点
有且只有一个交点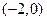 .
.当
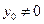 时得
时得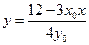 ,代入
,代入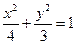 ,消去
,消去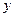 整理得:
整理得: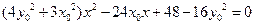 --------------------------------① ………………9分
--------------------------------① ………………9分由点
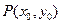 为曲线
为曲线 上一点,故
上一点,故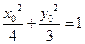 .即
.即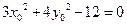
于是方程①可以化简为:
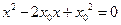
解得
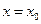 .将
.将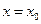 代入
代入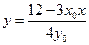 得
得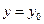 ,说明直线与曲线有且只有一个交点
,说明直线与曲线有且只有一个交点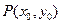 .
.综上,不论点
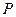 在何位置,直线
在何位置,直线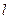 :
: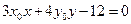 与曲线
与曲线 恒有且只有一个交点,交点即
恒有且只有一个交点,交点即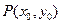 . ……………………………………………12分
. ……………………………………………12分略

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
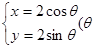 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,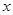 轴的正半轴
轴的正半轴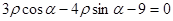 ,则直线与圆的位
,则直线与圆的位 ,动圆
,动圆 过点
过点 且与圆
且与圆 相切,记动圆圆
相切,记动圆圆 .
. 为曲线
为曲线 与曲线
与曲线 写出一个类似的结论(皆不必证明).
写出一个类似的结论(皆不必证明). 相切的圆的方程为
相切的圆的方程为



 ,圆
,圆 ,则其公共弦所在直线方程的斜率为
,则其公共弦所在直线方程的斜率为


 B相切,求a和b之间的关系式;
B相切,求a和b之间的关系式; )2=6上的动点,则
)2=6上的动点,则 的最大值为 ;
的最大值为 ;