题目内容
已知椭圆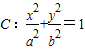 (a>b>0)的左顶点和右焦点分别为A,F,右准线为直线m,圆D:x2+y2-6y-4=0.
(a>b>0)的左顶点和右焦点分别为A,F,右准线为直线m,圆D:x2+y2-6y-4=0.(1)若点A在圆D上,且椭圆C的离心率为
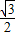 ,求椭圆C的方程;
,求椭圆C的方程;(2)若直线m上存在点Q,使△AFQ为等腰三角形,求椭圆C的离心率的取值范围;
(3)若点P在(1)中的椭圆C上,且过点P可作圆D的两条切线,切点分别为M、N,求弦长MN的取值范围.
【答案】分析:(1)对x2+y2-6y-4=0,令y=0,则x=±2.所以,A(-2,0),a=2,又因为,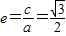 ,所以,
,所以,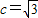 ,由此能够得到椭圆C的方程.
,由此能够得到椭圆C的方程.
(2)由△AFQ为等腰三角形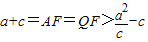 ,知2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0,又0<e<1,所以
,知2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0,又0<e<1,所以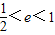 ,由此得到椭圆离心率取值范围.
,由此得到椭圆离心率取值范围.
(3)连PD交MN于H,连DM,则由圆的几何性质知:H为MN的中点,DM⊥PM,MN⊥PD.所以,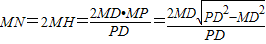 =
=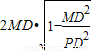 .⊙D:x2+(y-3)2=13,
.⊙D:x2+(y-3)2=13,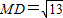 ,所以
,所以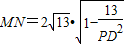 .由此能够求出弦长MN的取值范围.
.由此能够求出弦长MN的取值范围.
解答:解:(1)对x2+y2-6y-4=0,令y=0,则x=±2.
所以,A(-2,0),a=2(2分)
又因为,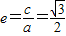 ,
,
所以, ,(3分)
,(3分)
b2=a2-c2=1(4分)
所以,椭圆C的方程为: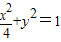 .(5分)
.(5分)
(2)由图知△AFQ为等腰三角形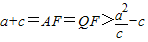 (7分)
(7分)
所以,2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0
又0<e<1,
所以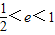 ,即椭圆离心率取值范围为
,即椭圆离心率取值范围为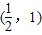 .(10分)
.(10分)
(3)连PD交MN于H,连DM,则由圆的几何性质知:H为MN的中点,DM⊥PM,MN⊥PD.
所以,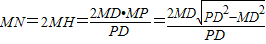
=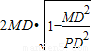
⊙D:x2+(y-3)2=13,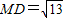
所以,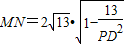 (13分)
(13分)
设P(x,y),则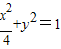 且-1≤y<0
且-1≤y<0
所以,PD2=x2+(y-3)2=-3y2-6y2+13=-3(y+1)2+16(-1≤y<0)
所以,13<PD2≤16(15分)
所以,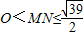 .(16分)
.(16分)
点评:本题考查圆锥曲线和直线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.
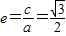 ,所以,
,所以,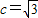 ,由此能够得到椭圆C的方程.
,由此能够得到椭圆C的方程.(2)由△AFQ为等腰三角形
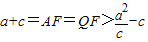 ,知2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0,又0<e<1,所以
,知2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0,又0<e<1,所以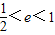 ,由此得到椭圆离心率取值范围.
,由此得到椭圆离心率取值范围.(3)连PD交MN于H,连DM,则由圆的几何性质知:H为MN的中点,DM⊥PM,MN⊥PD.所以,
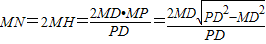 =
=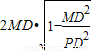 .⊙D:x2+(y-3)2=13,
.⊙D:x2+(y-3)2=13,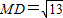 ,所以
,所以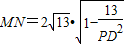 .由此能够求出弦长MN的取值范围.
.由此能够求出弦长MN的取值范围.解答:解:(1)对x2+y2-6y-4=0,令y=0,则x=±2.
所以,A(-2,0),a=2(2分)
又因为,
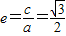 ,
,所以,
 ,(3分)
,(3分)b2=a2-c2=1(4分)
所以,椭圆C的方程为:
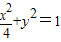 .(5分)
.(5分)(2)由图知△AFQ为等腰三角形
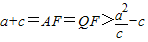 (7分)
(7分)所以,2c2+ac-a2>0,2e2+e-1>0,(2e-1)(e+1)>0
又0<e<1,
所以
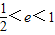 ,即椭圆离心率取值范围为
,即椭圆离心率取值范围为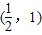 .(10分)
.(10分)(3)连PD交MN于H,连DM,则由圆的几何性质知:H为MN的中点,DM⊥PM,MN⊥PD.
所以,
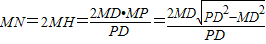
=
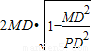
⊙D:x2+(y-3)2=13,
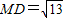
所以,
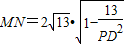 (13分)
(13分)设P(x,y),则
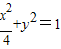 且-1≤y<0
且-1≤y<0所以,PD2=x2+(y-3)2=-3y2-6y2+13=-3(y+1)2+16(-1≤y<0)
所以,13<PD2≤16(15分)
所以,
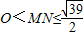 .(16分)
.(16分)点评:本题考查圆锥曲线和直线的位置关系,解题时要认真审题,注意挖掘题设中的隐含条件,合理地进行等价转化.

练习册系列答案
相关题目
 =1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
=1(a>b>0),F1、F2分别为椭圆的左、右焦点,A为椭圆的上的顶点,直线AF2交椭圆于另 一点B.
 =2
=2 ,
, ·
· =
= ,求椭圆的方程.
,求椭圆的方程. (a>b>0),点
(a>b>0),点 在椭圆上。
在椭圆上。 (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.