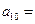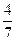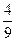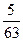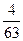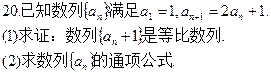题目内容
本小题满分12分)
已知数列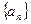 的前n项和为
的前n项和为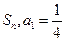 且
且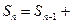
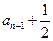 ,
,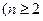 且
且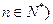 ,数列
,数列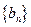 满足
满足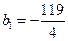 且
且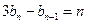
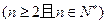 .
.
(I)求数列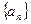 的通项公式;
的通项公式;
(II)求证:数列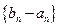 为等比数列;
为等比数列;
(III)求数列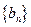 前
前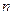 项和的最小值.
项和的最小值.
已知数列
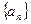 的前n项和为
的前n项和为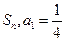 且
且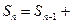
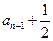 ,
,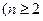 且
且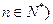 ,数列
,数列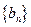 满足
满足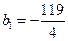 且
且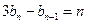
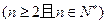 .
.(I)求数列
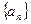 的通项公式;
的通项公式;(II)求证:数列
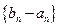 为等比数列;
为等比数列;(III)求数列
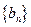 前
前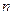 项和的最小值.
项和的最小值.解: (1)由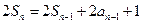 得
得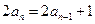 ,
, 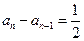 ……2分
……2分
∴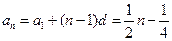 ………………4分
………………4分
(2)当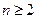 时 ∵
时 ∵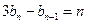 ,∴
,∴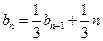 ,
,
∴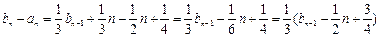 ;
;
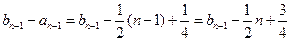 又
又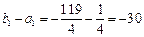
可证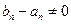 ∴由上面两式得
∴由上面两式得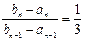 ,
,
∴数列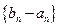 是以-30为首项,
是以-30为首项,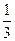 为公比的等比数列…………8分
为公比的等比数列…………8分
(3)由(2)得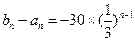 ,∴
,∴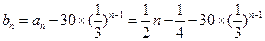
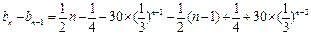
=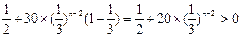 ,∴
,∴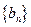 是递增数列 ………10分
是递增数列 ………10分
当n=1时,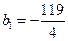 <0;当n=2时,
<0;当n=2时, 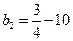 <0;当n=3时,
<0;当n=3时, 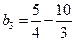 <0;当n=4时,
<0;当n=4时, 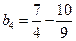 >0,所以,从
>0,所以,从 第4项起的各项均大于0,故前3项之和最小.
第4项起的各项均大于0,故前3项之和最小.
且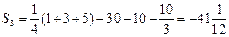 …………………………12分
…………………………12分
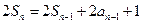 得
得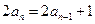 ,
, 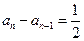 ……2分
……2分∴
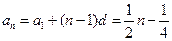 ………………4分
………………4分(2)当
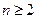 时 ∵
时 ∵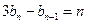 ,∴
,∴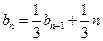 ,
,∴
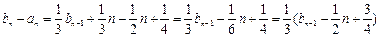 ;
;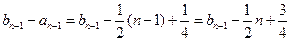 又
又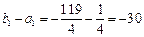
可证
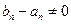 ∴由上面两式得
∴由上面两式得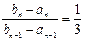 ,
,∴数列
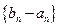 是以-30为首项,
是以-30为首项,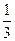 为公比的等比数列…………8分
为公比的等比数列…………8分(3)由(2)得
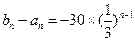 ,∴
,∴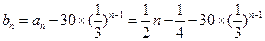
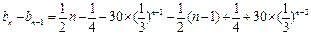
=
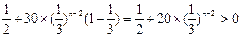 ,∴
,∴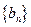 是递增数列 ………10分
是递增数列 ………10分当n=1时,
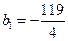 <0;当n=2时,
<0;当n=2时, 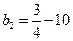 <0;当n=3时,
<0;当n=3时, 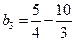 <0;当n=4时,
<0;当n=4时, 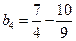 >0,所以,从
>0,所以,从 第4项起的各项均大于0,故前3项之和最小.
第4项起的各项均大于0,故前3项之和最小.且
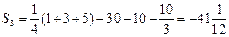 …………………………12分
…………………………12分略

练习册系列答案
相关题目
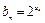 ,求数列{bn}的前n和Sn .
,求数列{bn}的前n和Sn .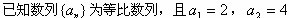

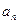 }的前n项和
}的前n项和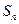 =2-
=2- }满足b1=1, b3+b7=18,且
}满足b1=1, b3+b7=18,且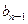 +
+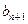 =2
=2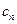 =
=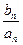 ,求数列{
,求数列{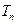 .
.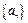 的公差为
的公差为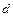 ,前
,前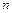 项的和为
项的和为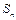 ,则数列
,则数列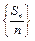 为等差数列,公差为
为等差数列,公差为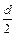 .类似地,若各项均为正数的等比数列
.类似地,若各项均为正数的等比数列 的公比为
的公比为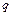 ,
, 前
前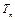 ,则数列
,则数列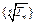 为等比数列,公比为 .
为等比数列,公比为 .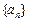 的公比大于1,
的公比大于1,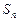 是数列
是数列 的前n项和,
的前n项和,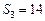 ,且
,且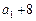 ,
,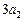 ,
,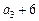 依次
依次 成等差数列,数列
成等差数列,数列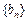 满足:
满足: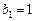 ,
,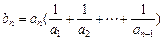
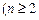 )
)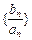 的前n项的和
的前n项的和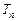 .
.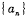 ,定义.
,定义.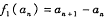 ,并对所有整数K >1定义
,并对所有整数K >1定义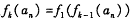 .若
.若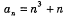 ,那么对所有
,那么对所有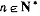 ,使得
,使得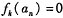 成立的k的最小值是_________
成立的k的最小值是_________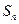 ,且
,且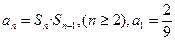 ,则
,则