题目内容
(本小题满分12分)
已知数列{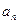 }的前n项和
}的前n项和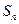 =2-
=2-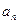 ,数列{
,数列{ }满足b1=1, b3+b7=18,且
}满足b1=1, b3+b7=18,且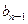 +
+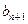 =2
=2 (n≥2).
(n≥2).
(Ⅰ)求数列{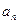 }和{
}和{ }的通项公式;
}的通项公式;
(Ⅱ)若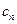 =
=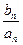 ,求数列{
,求数列{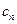 }的前n项和
}的前n项和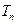 .
.
已知数列{
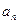 }的前n项和
}的前n项和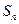 =2-
=2-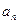 ,数列{
,数列{ }满足b1=1, b3+b7=18,且
}满足b1=1, b3+b7=18,且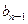 +
+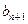 =2
=2 (n≥2).
(n≥2).(Ⅰ)求数列{
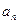 }和{
}和{ }的通项公式;
}的通项公式;(Ⅱ)若
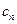 =
=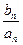 ,求数列{
,求数列{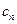 }的前n项和
}的前n项和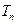 .
.解:⑴由题意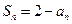 , ①
, ①
当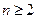 时,
时,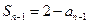 , ②
, ②
①-②得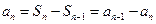 , 即
, 即 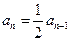 ,--------3分
,--------3分
又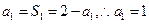 ,
,
故数列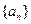 是以
是以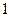 为首项,
为首项,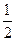 为公比的等比数列,所以
为公比的等比数列,所以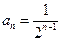 ;--------4分
;--------4分
由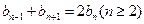 知,数列
知,数列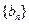 是等差数列,设其公差为
是等差数列,设其公差为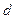 ,
,
则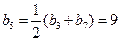 ,所以
,所以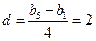 ,
,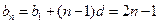 ;
;
综上,数列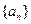 和
和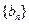 的通项公式为
的通项公式为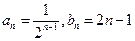 .--------7分
.--------7分
⑵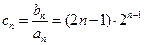 ,
,
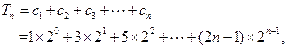 ③
③
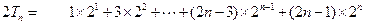 , ④
, ④
③-④得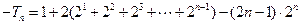 ,--------9分
,--------9分
整理得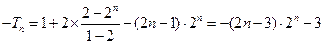 ,
,
所以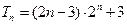 .--------12分
.--------12分
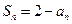 , ①
, ① 当
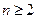 时,
时,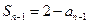 , ②
, ②①-②得
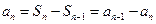 , 即
, 即 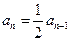 ,--------3分
,--------3分又
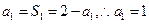 ,
,故数列
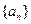 是以
是以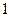 为首项,
为首项,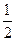 为公比的等比数列,所以
为公比的等比数列,所以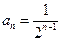 ;--------4分
;--------4分由
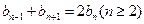 知,数列
知,数列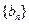 是等差数列,设其公差为
是等差数列,设其公差为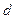 ,
,则
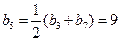 ,所以
,所以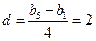 ,
,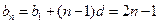 ;
;综上,数列
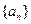 和
和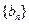 的通项公式为
的通项公式为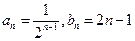 .--------7分
.--------7分⑵
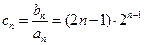 ,
,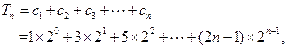 ③
③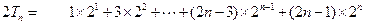 , ④
, ④③-④得
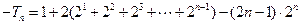 ,--------9分
,--------9分整理得
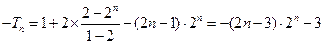 ,
,所以
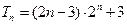 .--------12分
.--------12分略

练习册系列答案
相关题目
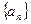 的前n项和为
的前n项和为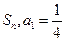 且
且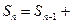
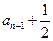 ,
,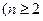 且
且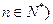 ,数列
,数列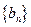 满足
满足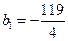 且
且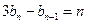
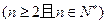 .
.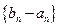 为等比数列;
为等比数列;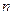 项和的最小值.
项和的最小值.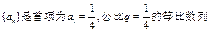 ,设
,设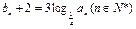 ,数列
,数列 。
。
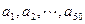 是从—1、0、1这三个整数中取值的数列,若
是从—1、0、1这三个整数中取值的数列,若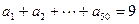 ,且
,且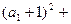
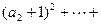
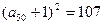 ,则
,则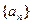 中,
中,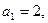 公积为5,当n为奇数时,这个数列的前
公积为5,当n为奇数时,这个数列的前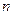 项和
项和 =_________。
=_________。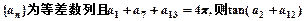 的值为 ( )
的值为 ( )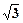
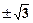
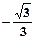
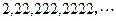 的一个通项公式
的一个通项公式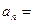 ______;
______; 中,
中,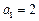 ,且有
,且有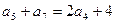 ,
, 则
则 ( )
( ) 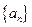 是等差数列, 若
是等差数列, 若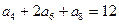 , 则该数列前11项的和为 .
, 则该数列前11项的和为 .