Question

（2011•黄冈模拟）已知D是由不等式组

x-y≥0 x+y≥0

所确定的平面区域，则圆x²+y²=4在区域D内的面积为（　　）

• A．2π
• B．π
• C．

  π

  2

• D．

  π

  4

Answer 1

分析：先依据不等式组

x-y≥0 x+y≥0

，结合二元一次不等式（组）与平面区域的关系画出其表示的平面区域，再利用圆的方程画出图形，最后利用扇形面积公式计算即可．

解答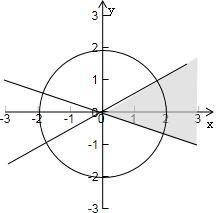：解：如图阴影部分表示

x-y≥0 x+y≥0

，确定的平面区域，所以阴影部分扇形即为所求．
∵直线x-y=0和直线x+y=0互相垂直，∴扇形的圆心角为90°，扇形的面积是圆的面积的四分之一，
∴圆x²+y²=4在区域D内的面积为π．
故选B．

点评：本题主要考查了用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．借助于平面区域特性，用几何方法处理代数问题，体现了数形结合思想、化归思想．