题目内容
.已知关于x的一元二次方程x -2(a-2)x-b
-2(a-2)x-b +16=0.
+16=0.
(1)若a、b是一枚骰子先后投掷两次所得到的点数,求方程有两个正实数根的概率;
(2)若a∈[2,6],b∈[0,4],求一元二次方程没有实数根的概率
【答案】
(1)P(A)= 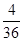 =
=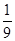 .(2) P(B)=
.(2) P(B)= 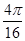 =
=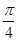
【解析】本题考查等可能事件的概率,在解题过程中主要应用列举法来列举出所有的满足条件的事件数,这是本题的精华部分.
(1)基本事件(a,b)共有36个,且a,b∈{1,2,3,4,5,6},方程有两个证实数根等价于a-2>0,16- 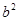 >0,△≥0,即a>2,-4<b<4,
>0,△≥0,即a>2,-4<b<4, 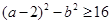 得到符合题意的事件的基本事件数为4个,故可以求解得到。
得到符合题意的事件的基本事件数为4个,故可以求解得到。
(2)设“一元二次方程无实数根”为事件B,则构成事件B的区域为
B={(a,b)∣2≤a≤6,0≤b≤4,  <16},利用面积比得到概率值。
<16},利用面积比得到概率值。
解:(1)基本事件(a,b)共有36个,且a,b∈{1,2,3,4,5,6},方程有两个证实数根等价于a-2>0,16- 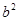 >0,△≥0,即a>2,-4<b<4,
>0,△≥0,即a>2,-4<b<4, 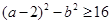
设”一元二次方程有两个正实数根“为事件A,则事件A所包含的基本事件为(6,1),(6,2),(6,3),(5,3)共4个,故所求概率为P(A)= 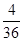 =
=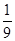 .
.
(2)设“一元二次方程无实数根”为事件B,则构成事件B的区域为
B={(a,b)∣2≤a≤6,0≤b≤4,  <16},其面积为S(B)=
<16},其面积为S(B)= 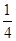 ×
× ×
×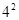 =4
=4 ,故所求概率为P(B)=
,故所求概率为P(B)= 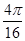 =
=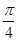

练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目