题目内容
(1)在一个红绿灯路口,红灯、黄灯和绿灯的时间分别为30秒、5秒和40秒.当你到达路口时,求不是红灯的概率.(2)已知关于x的一元二次函数f(x)=ax2-4bx+1.设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
分析:(1)这是一个与长度有关的几何概率,不满足条件的时间长度为30秒,总的时间长度为30+5+40秒,我们可以求出红灯出现的概率,然后根据对立事件减法公式求出不是红灯的概率;
(2)这是一个古典概型问题,我们分别计算出满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式,即可求解.
(2)这是一个古典概型问题,我们分别计算出满足条件的基本事件个数,及基本事件的总个数,然后代入古典概型计算公式,即可求解.
解答:解:(1)基本事件是遇到红灯、黄灯和绿灯,它们的时间分别为30秒、5秒和40秒,设它们的概率的分别为P1,P2,P3,
所以不是红灯的概率P=1-P1=1-
=
(2)∵函数f(x)=ax2-4bx+1的图象的对称轴为x=
要使f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且
≤1,即2b≤a
若a=1则b=-1,
若a=2则b=-1,1;
若a=3则b=-1,1;
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
=
所以不是红灯的概率P=1-P1=1-
| 30 |
| 30+5+40 |
| 3 |
| 5 |
(2)∵函数f(x)=ax2-4bx+1的图象的对称轴为x=
| 2b |
| a |
要使f(x)=ax2-4bx+1在区间[1,+∞)上为增函数,
当且仅当a>0且
| 2b |
| a |
若a=1则b=-1,
若a=2则b=-1,1;
若a=3则b=-1,1;
∴事件包含基本事件的个数是1+2+2=5
∴所求事件的概率为
| 5 |
| 15 |
| 1 |
| 3 |
点评:本题考查的是几何概型和古典概型,掌握几何概型和古典概型的计算步骤和计算公式是解答本题的关键.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
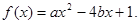 设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为
设集合P={1,2,3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为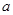 和
和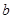 ,求函数
,求函数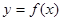 在区间[
在区间[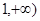 上是增函数的概率.
上是增函数的概率.