题目内容

设△ABC的内角A，B，C所对的边分别为a，b，c，若bcos C＋ccos B＝asin A，则△ABC的形状为(　　)．

A．锐角三角形 B．直角三角形

C．钝角三角形 D．不确定

 

B

【解析】由bcos C＋ccos B＝asin A，得sin Bcos C＋sin Ccos B＝sin2A，即sin(B＋C)＝sin2A，所以sin A＝1，由0<A<π，得A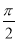＝，所以△ABC为直角三角形．

 

练习册系列答案
相关题目

已知以角为钝角的的内角的对边分别为、、，，且与垂直。

（1）求角的大小；

（2）求的取值范围．

 

已知向量的夹角为．

（1）求的值；

（2）求的大小．

 

已知{an}是等差数列，a1＝1，公差d≠0，Sn为其前n项和，若a1，a2，a5成等比数列，则S8＝________.

 

已知点A(－1,1)，B(1,2)，C(－2，－1)，D(3,4)，则向量在方向上的投影为(　　)

A. B. C.－ D．－

 

函数f(x)＝2sin(ωx＋φ)(ω>0，－<φ<)的部分图象如图所示，则ω，φ的值分别是(　　)．

A．2，－ B．2，－ C．4，－ D．4，

 

设函数f(x)的定义域为R，x0(x0≠0)是f(x)的极大值点，以下结论一定正确的是(　　)．

A．?x∈R，f(x)≤f(x0)

B．－x0是f(－x)的极小值点

C．－x0是－f(x)的极小值点

D．－x0是－f(－x)的极小值点

 

已知中心在原点的双曲线C的右焦点为F(3,0)，离心率等于，则C的方程是(　　)．

A. ＝1 B. ＝1 C. ＝1 D. ＝1

 

设f(x)是周期为2的奇函数，当0≤x≤1时，f(x)＝2x(1－x)，则f=(　)．

A．－ B．－ C. D.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网