题目内容
O为平面上的定点，A、B、C是平面上不共线的三点，若（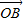
-
）•（
+
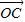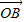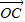-2
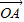）=0，则△DABC是 三角形．
【答案】分析：首先把2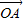
拆开分别与
、
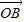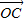组合，再由向量加减运算即可整理，然后根据
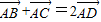（点D为线段BC的中点．），并结合图形得出结论．
解答：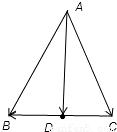
解：由题意知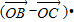
=
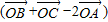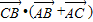=0，
如图所示，其中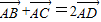
（点D为线段BC的中点），
所以AD⊥BC，即AD是BC的中垂线，
所以AB=AC，即△ABC为等腰三角形．
故答案为“以BC为底边的等腰三角形”．
点评：本题主要考查向量加、减法的运算及几何意义，同时考查向量垂直的条件．
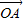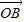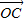拆开分别与、组合，再由向量加减运算即可整理，然后根据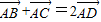（点D为线段BC的中点．），并结合图形得出结论．解答：
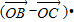
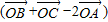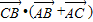解：由题意知==0，如图所示，其中
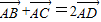（点D为线段BC的中点），所以AD⊥BC，即AD是BC的中垂线，
所以AB=AC，即△ABC为等腰三角形．
故答案为“以BC为底边的等腰三角形”．
点评：本题主要考查向量加、减法的运算及几何意义，同时考查向量垂直的条件．
练习册系列答案
相关题目
-
)?(
)=0，则DABC是（ ）
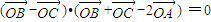，则△ABC是（ ）