题目内容
设m为实数,函数f(x)=-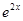 +2x+m,x∈R
+2x+m,x∈R
(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当m≤1且x>0时,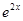 >2
>2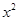 +2mx+1.
+2mx+1.
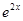 +2x+m,x∈R
+2x+m,x∈R(Ⅰ)求f(x)的单调区间与极值;
(Ⅱ)求证:当m≤1且x>0时,
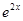 >2
>2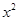 +2mx+1.
+2mx+1.(Ⅰ)增区间 ,减区间
,减区间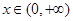 ;(Ⅱ)构造函数
;(Ⅱ)构造函数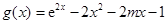 ,再证明
,再证明 即可得证.
即可得证.
 ,减区间
,减区间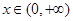 ;(Ⅱ)构造函数
;(Ⅱ)构造函数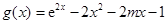 ,再证明
,再证明 即可得证.
即可得证.试题分析:(Ⅰ)利用求导的方法求得单调区间,再求极值;(Ⅱ)先构造
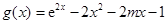 ,
,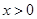 ,再证得
,再证得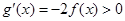 ,即
,即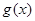 在
在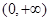 上为增函数,所以
上为增函数,所以 ,故
,故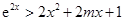 .
.试题解析:(Ⅰ)
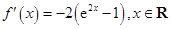 ,令
,令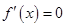 可得
可得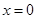 ,
,易知
 时
时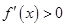 ,
,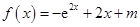 为增函数,
为增函数,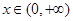 时
时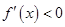 ,
,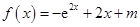 为减函数,
为减函数,所以函数
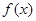 有极大值,无极小值,极大值为
有极大值,无极小值,极大值为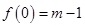 . (6分)
. (6分)(Ⅱ)令
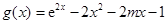 ,
,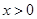 ,则
,则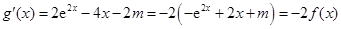 ,
,由(Ⅰ)知,当
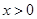 时,
时, 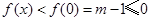 ,所以
,所以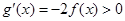 ,
,故
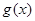 在
在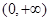 上为增函数,
上为增函数,所以
 ,故
,故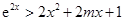 . (12分)
. (12分)
练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
 ,
, ,且
,且 在点(1,
在点(1, )处的切线方程为
)处的切线方程为 。
。 的单调递增区间;
的单调递增区间; ,若方程
,若方程 有且仅有四个解,求实数a的取值范围。
有且仅有四个解,求实数a的取值范围。 .
. 时,求曲线
时,求曲线 在
在 处的切线方程;
处的切线方程;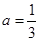 时,求函数
时,求函数 ,若对于
,若对于 [1,2],
[1,2], [0,1],使
[0,1],使 成立,求实数
成立,求实数 的取值范围.
的取值范围.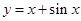 在点
在点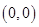 处的切线方程是 .
处的切线方程是 .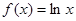 ,且
,且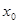 ,
,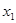 ,
,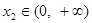 ,下列命题:
,下列命题: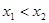 ,则
,则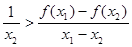
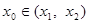 ,
,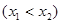 ,使得
,使得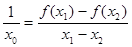
 ,
,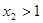 ,则
,则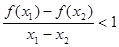
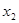 ,都有
,都有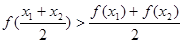
 在点
在点 处的切线与直线
处的切线与直线 平行,则点
平行,则点



 的图像在点
的图像在点 处的切线斜率为
处的切线斜率为 ,则
,则 的值是 .
的值是 .
 的单调区间;
的单调区间; 在
在 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 成立,求实数
成立,求实数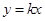 是
是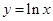 的切线,则
的切线,则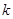 的值是 .
的值是 .