题目内容
在平面直角坐标系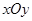 中,以
中,以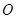 为极点,
为极点,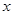 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线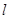 的极坐标方程为
的极坐标方程为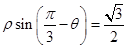 ,曲线
,曲线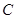 的参数方程为
的参数方程为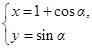 (
(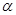 为参数,
为参数,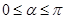 ).
).
(1)写出直线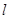 的直角坐标方程;
的直角坐标方程;
(2)求直线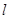 与曲线
与曲线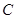 的交点的直角坐标.
的交点的直角坐标.
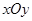 中,以
中,以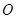 为极点,
为极点,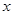 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线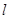 的极坐标方程为
的极坐标方程为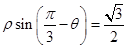 ,曲线
,曲线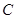 的参数方程为
的参数方程为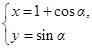 (
(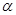 为参数,
为参数,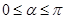 ).
).(1)写出直线
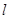 的直角坐标方程;
的直角坐标方程;(2)求直线
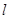 与曲线
与曲线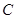 的交点的直角坐标.
的交点的直角坐标.(1)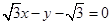 ;(2)
;(2)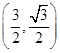 .
.
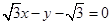 ;(2)
;(2)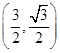 .
.试题分析:本小题主要考查直线的极坐标方程、圆的参数方程及其几何意义、直线与圆的位置关系、极直互化等基础知识;考查运算求解能力;数形结合思想.第一问,利用极坐标与直角坐标的互化公式
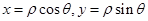 ,转化方程;第二问,先将曲线C的参数方程转化为普通方程,得到圆,再令直线与圆的方程联立求交点.
,转化方程;第二问,先将曲线C的参数方程转化为普通方程,得到圆,再令直线与圆的方程联立求交点.试题解析:(1)∵
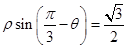 ,∴
,∴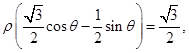 1分
1分∴
 即所求直线
即所求直线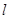 的直角坐标方程为
的直角坐标方程为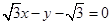 . 3分
. 3分(2)曲线
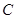 的直角坐标方程为:
的直角坐标方程为: , 4分
, 4分∴
 ,解得
,解得 或
或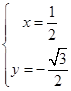 (舍去). 6分
(舍去). 6分所以,直线
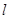 与曲线
与曲线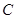 的交点的直角坐标为
的交点的直角坐标为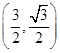 . 7分
. 7分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
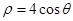 ,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是
,以极点为平面直角坐标系的原点,极轴为轴的正半轴建立平面直角坐标系,直线L的参数方程是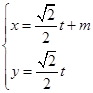 (t是参数)
(t是参数)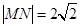 ,求实数m的值.
,求实数m的值.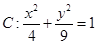 ,直线
,直线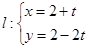 (
(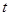 为参数)
为参数)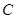 的参数方程,直线
的参数方程,直线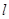 的普通方程;
的普通方程;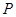 作与
作与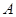 ,求
,求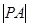 的最大值与最小值.
的最大值与最小值.
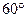
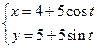 (t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为
(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为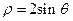 .
.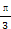 )且和极轴成
)且和极轴成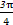 角的直线.
角的直线.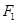 是椭圆
是椭圆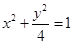 的下焦点,
的下焦点,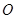 为坐标原点,点
为坐标原点,点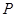 在椭圆上,则
在椭圆上,则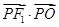 的最大值为
的最大值为 .
.