题目内容
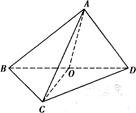
如图,在三棱锥A-BCD中,△ABD和△BCD是两个全等的等腰直角三角形,O为BD的中点,且AB=AD=CB=CD=2,AC= .
.
(1)当 时,求证:AO⊥平面BCD;
时,求证:AO⊥平面BCD;
(2)当二面角 的大小为
的大小为 时,求二面角
时,求二面角 的正切值.
的正切值.
(1)先证 AO⊥CO,
AO⊥BD (2)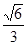
【解析】
试题分析:(1)根据题意知,在△AOC中, ,
,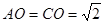 ,
,
所以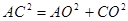 ,所以AO⊥CO.
,所以AO⊥CO.
因为AO是等腰直角E角形ABD的中线,所以AO⊥BD.
又BD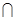 CO=O,所以AO⊥平面BCD.
CO=O,所以AO⊥平面BCD.
(2)法一 由题易知,CO⊥OD.如图,以O为原点,
OC、OD所在的直线分别为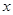 轴、
轴、 轴建立如图所示的空间直角坐标系
轴建立如图所示的空间直角坐标系 ,
,
则有O(0,0,0),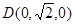 ,
,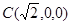 ,
, .
.
设 ,则
,则
 ,
,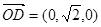 .
.
设平面ABD的法向量为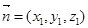 ,
,

则 即
即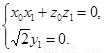
所以 ,令
,令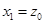 ,则
,则 .
.
所以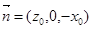 .
.
因为平面BCD的一个法向量为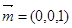 ,
,
且二面角 的大小为
的大小为 ,所以
,所以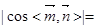
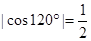 ,
,
即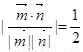 ,整理得
,整理得 .
.
因为 ,所以
,所以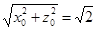 ,
,
解得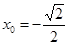 ,
, ,所以
,所以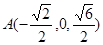 ,
,
设平面ABC的法向量为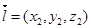 ,
,
因为 ,
, ,
,
则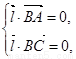 即
即
令 ,则
,则 ,
,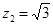 .所以
.所以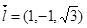 .
.
设二面角 的平面角为
的平面角为 ,则
,则

 .
.
所以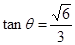 ,即二面角
,即二面角 的正切值为
的正切值为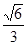 .
.
法二 在△ABD中,BD⊥AO,在△BCD中,BD⊥CO,
所以∠AOC是二面角 的平面角,即∠AOC=
的平面角,即∠AOC= .
.
如图,过点A作CO的垂线交CO的延长线于点H,
因为BD⊥CO,BD⊥AO,且CO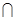 AO=O,
AO=O,
所以BD⊥平面AOC.
因为AH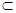 平面AOC,所以BD⊥AH.
平面AOC,所以BD⊥AH.
又CO⊥AH,且CO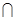 BD=O,所以AH⊥平面BCD.
BD=O,所以AH⊥平面BCD.
过点A作AK⊥BC,垂足为K,连接HK.
因为BC⊥AH,AK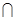 AH=A,所以BC⊥平面AHK.
AH=A,所以BC⊥平面AHK.
因为HK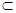 平面AHK,所以BC⊥HK,
平面AHK,所以BC⊥HK,
所以∠AKH为二面角 的平面角.
的平面角.
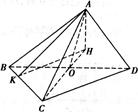
在△AOH中,∠AOH= ,
, ,则
,则 ,
,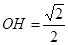 ,
,
所以 .
.
在R t△CHK中,∠HCK= ,所以
,所以 .
.
在 R t△AHK中,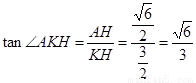 ,
,
所以二面角 的正切值为
的正切值为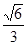 .
.
考点:直线与平面垂直的判定;与二面角有关的立体几何综合题.
点评:本小题主要考查空间线面关系、二面角的度量、直线与平面所成的角等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

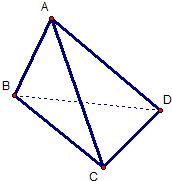 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=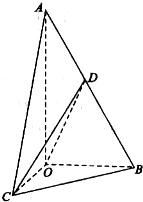 如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4,
如图,在三棱锥A-BOC中,AO⊥底面BOC,∠OAB=∠OAC=30°,AB=AC=4, 如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC.
如图,在三棱锥A-BCD中,AD⊥平面ABC,∠BAC=120°,且AB=AC=AD=2,点E在BC上,且AE⊥AC. 如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,
如图,在三棱锥A-BOC中,AO⊥面BOC,二面角B-AO-C是直二面角,OB=OC,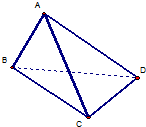 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=