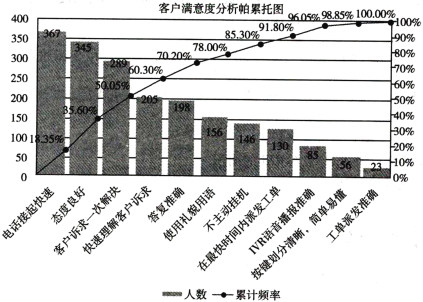
ЬтФПФкШн
ЁОЬтФПЁПЁАЖтЛ§ЪѕЁБЪЧЮвЙњЙХДњЪ§бЇЕФживЊГЩОЭжЎвЛ.ФЯЫЮЪ§бЇМвбюЛддкЁЖЯъНтОХеТЫуЗЈЁЗжаМЧдиСЫЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃКЁАЙћзгвдЖтЃЌЯТЗНЪЎЫФИіЃЌЮЪМЦМИКЮЃПЪѕдЛЃКЯТЗНМгвЛЃЌГЫЯТЗНЮЊЦНЛ§.гжМгАыЮЊИпЃЌвдГЫЯТЗНЮЊИпЛ§.ШчШ§ЖјвЛ.ЁБвтЫМЪЧЫЕЃЌНЋЙћзгвдЗНЖтЕФаЮЪНАкЗХЃЈЗНЖтМДУПВуОљЮЊе§ЗНаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЃЌзюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЃЌЮЪЙВгаЖрЩйИіЙћзгЃПМЦЫуЗНЗЈгУЫуЪНБэЪОЮЊ![]() .РћгУЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃЌПЩМЦЫузюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЕФЁАШ§НЧЖтЁБЃЈШ§НЧЖтМДУПВуОљЮЊе§Ш§НЧаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЙВгаЙћзгЪ§ЮЊЃЈ ЃЉ
.РћгУЁАЗНЖтЁБЕФМЦЫуЗНЗЈЃЌПЩМЦЫузюЯТВуУПБпЙћзгЪ§ЮЊ14ИіЕФЁАШ§НЧЖтЁБЃЈШ§НЧЖтМДУПВуОљЮЊе§Ш§НЧаЮЃЌздЯТЖјЩЯУПВуУПБпЙћзгЪ§вРДЮЕнМѕ1ИіЃЌзюЩЯВуЮЊ1ИіЃЉЙВгаЙћзгЪ§ЮЊЃЈ ЃЉ
A.420ИіB.560ИіC.680ИіD.1015Иі
ЁОД№АИЁПB
ЁОНтЮіЁП
гЩЬтвтПЩЕУЃЌзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ
ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌдйгЩзюЯТВуУПБпЮЊ
ЃЌдйгЩзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАШ§НЧВйЁБздЩЯЖјЯТЕФЕк
ИіЙћзгЕФЁАШ§НЧВйЁБздЩЯЖјЯТЕФЕк![]() ВуЙћзгЪ§ЮЊ
ВуЙћзгЪ§ЮЊ![]() ЃЌЕУ
ЃЌЕУ![]() ВуЁАШ§НЧВйЁБзмЕФЙћзгЪ§ЮЊ
ВуЁАШ§НЧВйЁБзмЕФЙћзгЪ§ЮЊ![]() ЃЌзюКѓгУЗжзщЧѓКЭЕФЗНЗЈМДПЩЧѓНт.
ЃЌзюКѓгУЗжзщЧѓКЭЕФЗНЗЈМДПЩЧѓНт.
гЩЬтвтжЊЃЌзюЯТВуУПБпЮЊ14ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌ
ЃЌ
ЫљвдПЩЕУзюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ
ИіЙћзгЕФЁАЗНЖтЁБзмЕФЙћзгЪ§ЕФМЦЫуЪНЮЊ![]() ЃЌ
ЃЌ
зюЯТВуУПБпЮЊ![]() ИіЙћзгЕФЁАШ§НЧЖтЁБздЩЯЖјЯТЕФЕк
ИіЙћзгЕФЁАШ§НЧЖтЁБздЩЯЖјЯТЕФЕк![]() ВуЙћзгЪ§ЮЊ
ВуЙћзгЪ§ЮЊ![]() ЃЌЫљвд
ЃЌЫљвд![]() ВуЁАШ§НЧЖтЁБзмЕФЙћзгЪ§ЮЊ
ВуЁАШ§НЧЖтЁБзмЕФЙћзгЪ§ЮЊ![]() ЃЌвђЮЊ
ЃЌвђЮЊ
![]()
![]()
![]()
![]()
![]() ЃЌ
ЃЌ
ЫљвдШЁ![]() ЃЌПЩЕУЁАШ§НЧЖтЁБЕФЙћзгзмЪ§ЮЊ560Иі.
ЃЌПЩЕУЁАШ§НЧЖтЁБЕФЙћзгзмЪ§ЮЊ560Иі.
ЙЪбЁЃКB

 жЧШЄЪюМйЮТЙЪжЊаТЯЕСаД№АИ
жЧШЄЪюМйЮТЙЪжЊаТЯЕСаД№АИ