题目内容
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:①恒有直线BC∥平面A′DE;
②恒有直线DE⊥平面A′FG;
③恒有平面A′FG⊥平面A′DE.
其中正确命题的序号为 .

【答案】分析:由△ABC为正三角形,DE是其中位线,可探讨BC与DE的位置关系,以及直线 DE与AF,A′G的位置关系,从而可以得到①②③正确与否.
解答: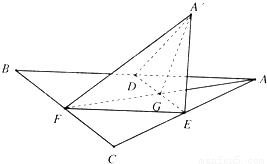 解:如图,正△ABC的中线AF与中位线DE相交于点G,
解:如图,正△ABC的中线AF与中位线DE相交于点G,
已知△A′DE是△ADE绕边DE旋转形成的一个图形,
且A′∉平面ABC,
∴△ABC为正三角形且中线AF与中位线DE相交,
∴BC∥DE,又BC?平面A′DE,DE?平面A′DE,
∴BC∥平面A′DE,故①对;
又AG⊥DE,A′G⊥DE,
且AG∩A′G=G
∴DE⊥面A′FG,故②对
∵DE?面A′DE,
∴平面A′FG⊥平面A′DE,故③对;
故答案为:①②③.
点评:本题主要考查了命题的真假判断与应用,考查空间中点,线,面的位置关系,以及线面,面面垂直的判断和性质,是个基础题.
解答:
 解:如图,正△ABC的中线AF与中位线DE相交于点G,
解:如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,
且A′∉平面ABC,
∴△ABC为正三角形且中线AF与中位线DE相交,
∴BC∥DE,又BC?平面A′DE,DE?平面A′DE,
∴BC∥平面A′DE,故①对;
又AG⊥DE,A′G⊥DE,
且AG∩A′G=G
∴DE⊥面A′FG,故②对
∵DE?面A′DE,
∴平面A′FG⊥平面A′DE,故③对;
故答案为:①②③.
点评:本题主要考查了命题的真假判断与应用,考查空间中点,线,面的位置关系,以及线面,面面垂直的判断和性质,是个基础题.

练习册系列答案
 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
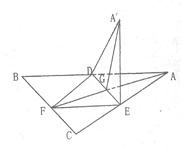 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.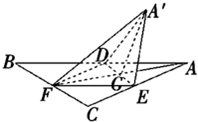 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( ) 如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题: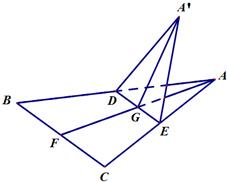 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )