题目内容
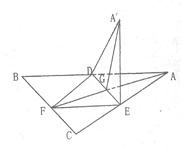 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.(I)求证点A′在平面ABC上的射影在线段AF上;
(II)求当A′E⊥BD时△A′DE所转过的角的大小.
分析:(I)根据线面垂直的判定定理可知DE⊥平面A'GA,而DE∥A'H从而得到A'H⊥平面ABC,最终说明了点A′在平面ABC上的射影在线段AF上;
(II)易知点H为正△ADE的中心,根据二面角平面角的定义可知∠A'GA是二面角A'-DE-A的平面角,在三角形而A'GA中求出此角,而二面角A'-DE-A的大小即为当AE⊥BD时,△A'DE所旋转过的角的大小.
(II)易知点H为正△ADE的中心,根据二面角平面角的定义可知∠A'GA是二面角A'-DE-A的平面角,在三角形而A'GA中求出此角,而二面角A'-DE-A的大小即为当AE⊥BD时,△A'DE所旋转过的角的大小.
解答:解:(I)在平面A’FA内过点A’作A’H⊥AF,垂足为H
因为DE⊥AF,DE⊥A'G?DE⊥平面A'GA(4分)
所以DE∥A'H?A'H⊥平面ABC(6分)
即点A′在平面ABC上的射影在线段AF上(7分)
(II)由(I)知A'H⊥平面ABC,
又A′E⊥BD,所以EH⊥BD(9分)
则点H为正△ADE的中心,所以HG=
AG=
A'G
因为DE⊥AF,DE⊥A'G?∠A'GA是二面角A'-DE-A的平面角.(11分)
而cos∠A′GA=
=
,
所以二面角A'-DE-A的大小为arccos
(13分)
二面角A'-DE-A的大小即为当AE⊥BD时,△A'DE所旋转过的角的大小.
故所求角等于arccos
(14分)
因为DE⊥AF,DE⊥A'G?DE⊥平面A'GA(4分)
所以DE∥A'H?A'H⊥平面ABC(6分)
即点A′在平面ABC上的射影在线段AF上(7分)
(II)由(I)知A'H⊥平面ABC,
又A′E⊥BD,所以EH⊥BD(9分)
则点H为正△ADE的中心,所以HG=
| 1 |
| 3 |
| 1 |
| 3 |
因为DE⊥AF,DE⊥A'G?∠A'GA是二面角A'-DE-A的平面角.(11分)
而cos∠A′GA=
| HG |
| A′G |
| 1 |
| 3 |
所以二面角A'-DE-A的大小为arccos
| 1 |
| 3 |
二面角A'-DE-A的大小即为当AE⊥BD时,△A'DE所旋转过的角的大小.
故所求角等于arccos
| 1 |
| 3 |
点评:本题主要考查了平面与平面之间的位置关系,以及二面角的度量,考查空间想象能力,几何逻辑推理能力,以及计算能力.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
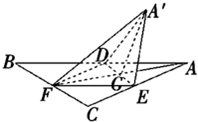 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( ) 如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题: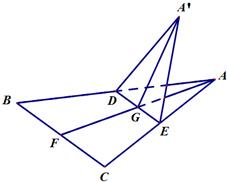 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )