题目内容
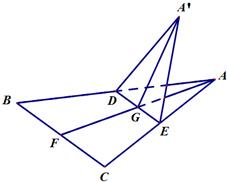 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′DE是△ADE绕DE旋转过程中的一个图形,下列命题中,错误的是( )分析:由斜线的射影定理可判断A正确;由面面垂直的判定定理,可判断B正确;由面面角的定义,可判断C正确;由异面直线所成的角的概念可判断D不正确
解答:解:∵A′D=A′E,△ABC是正三角形,∴A'在平面ABC上的射影在线段AF上,故A正确
由A知,平面A'GF一定过平面BCED的垂线,∴恒有平面A'GF⊥平面BCED,故B正确
由于正△ABC的中线AF与中位线DE,故可知A′G⊥DE,FG⊥DE,故C正确
当(A'E)2+EF2=(A'F)2时,直线A'E与BD垂直,故D不正确
故选D.
由A知,平面A'GF一定过平面BCED的垂线,∴恒有平面A'GF⊥平面BCED,故B正确
由于正△ABC的中线AF与中位线DE,故可知A′G⊥DE,FG⊥DE,故C正确
当(A'E)2+EF2=(A'F)2时,直线A'E与BD垂直,故D不正确
故选D.
点评:本题平面图形的旋转为载体,综合考查线面、面面垂直的判定定理、性质定理的运用,考查空间线线、线面的位置关系及所成的角的概念,考查空间想象能力,属中档题

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
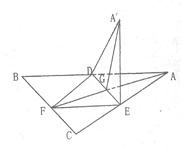 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△AED绕边DE旋转过程中的一个图形.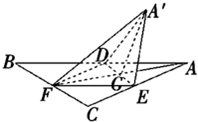 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列说法中,错误的是( ) 如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题:
如图,正△ABC的中线AF与中位线DE相交于G,已知△A'ED是△AED绕DE旋转过程中的一个图形,现给出下列四个命题: 如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题:
如图,正△ABC的中线AF与中位线DE相交于点G,已知△A′DE是△ADE绕边DE旋转形成的一个图形,且A′∉平面ABC,现给出下列命题: