题目内容
(2013•黑龙江二模)已知函数f(x)=lnx,x1,x2∈(0,
),且x1<x2,则下列结论中正确的是( )
| 1 |
| e |
分析:根据函数的单调性可得A不正确;根据函数的图象是下凹的,可得B不正确; 利用导数判断函数
在(0,+∞)上是增函数,故有
>
,
化简可得 x1f(x2)>x2f(x1),故C正确、且D不正确.
| f(x) |
| x |
| f(x2) |
| x2 |
| f(x1) |
| x1 |
化简可得 x1f(x2)>x2f(x1),故C正确、且D不正确.
解答:解:由于已知函数f(x)=lnx在定义域(0,+∞)上是增函数,x1,x2∈(0,
),且x1<x2 ,可得[f(x1)-f(x2)]<0,
故(x1-x2)[f(x1)-f(x2)]>0,故A不正确.
由于已知函数f(x)=lnx的增长速度较慢,图象是下凹型的,故有f(
)>f(
),故B不正确.
∵已知函数f(x)=lnx,x1,x2∈(0,
),且x1<x2 ,则 [
]′=
=
>0,
∴函数
在(0,+∞)上是增函数,故有
>
,化简可得 x1f(x2)>x2f(x1),故C正确、且D不正确.
故选C.
| 1 |
| e |
故(x1-x2)[f(x1)-f(x2)]>0,故A不正确.
由于已知函数f(x)=lnx的增长速度较慢,图象是下凹型的,故有f(
| x1+x2 |
| 2 |
| f(x1)+f(x2) |
| 2 |
∵已知函数f(x)=lnx,x1,x2∈(0,
| 1 |
| e |
| f(x) |
| x |
| f′(x)x-f(x) |
| x2 |
| 1-lnx |
| x2 |
∴函数
| f(x) |
| x |
| f(x2) |
| x2 |
| f(x1) |
| x1 |
故选C.
点评:本题主要考查导数的运算法则的应用,利用导数研究函数的单调性,函数的单调性的应用,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 (2013•黑龙江二模)某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是( )
(2013•黑龙江二模)某几何体的三视图 (单位:cm) 如图所示,则此几何体的体积是( )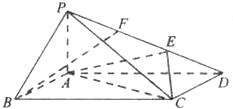 (2013•黑龙江二模)如图,在四棱锥P-ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.
(2013•黑龙江二模)如图,在四棱锥P-ABCD中,侧棱PA丄底面ABCD底面ABCD为矩形,E为PD上一点,AD=2AB=2AP=2,PE=2DE.